{
"cells": [
{
"cell_type": "markdown",
"id": "cf7afdb7",
"metadata": {},
"source": [
"\n",
""
]
},
{
"cell_type": "markdown",
"id": "3192041e",
"metadata": {},
"source": [
"# Globalization and Cycles"
]
},
{
"cell_type": "markdown",
"id": "60db9dbf",
"metadata": {},
"source": [
"## Overview\n",
"\n",
"In this lecture, we review the paper [Globalization and Synchronization of Innovation Cycles](http://www.centreformacroeconomics.ac.uk/Discussion-Papers/2015/CFMDP2015-27-Paper.pdf) by [Kiminori Matsuyama](http://faculty.wcas.northwestern.edu/~kmatsu/), [Laura Gardini](http://www.mdef.it/index.php?id=32) and [Iryna Sushko](http://irynasushko.altervista.org/).\n",
"\n",
"This model helps us understand several interesting stylized facts about the world economy.\n",
"\n",
"One of these is synchronized business cycles across different countries.\n",
"\n",
"Most existing models that generate synchronized business cycles do so by assumption, since they tie output in each country to a common shock.\n",
"\n",
"They also fail to explain certain features of the data, such as the fact that the degree of synchronization tends to increase with trade ties.\n",
"\n",
"By contrast, in the model we consider in this lecture, synchronization is both endogenous and increasing with the extent of trade integration.\n",
"\n",
"In particular, as trade costs fall and international competition increases, innovation incentives become aligned and countries synchronize their innovation cycles.\n",
"\n",
"Let’s start with some imports:"
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "4cb7ea52",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"from numba import jit\n",
"from ipywidgets import interact"
]
},
{
"cell_type": "markdown",
"id": "b2acd65d",
"metadata": {},
"source": [
"### Background\n",
"\n",
"The model builds on work by Judd [[Judd, 1985](https://python-advanced.quantecon.org/zreferences.html#id90)], Deneckner and Judd [[Deneckere and Judd, 1992](https://python-advanced.quantecon.org/zreferences.html#id89)] and Helpman and Krugman [[Helpman and Krugman, 1985](https://python-advanced.quantecon.org/zreferences.html#id91)] by developing a two-country model with trade and innovation.\n",
"\n",
"On the technical side, the paper introduces the concept of [coupled oscillators](https://en.wikipedia.org/wiki/Oscillation#Coupled_oscillations) to economic modeling.\n",
"\n",
"As we will see, coupled oscillators arise endogenously within the model.\n",
"\n",
"Below we review the model and replicate some of the results on synchronization of innovation across countries."
]
},
{
"cell_type": "markdown",
"id": "972684a2",
"metadata": {},
"source": [
"## Key Ideas\n",
"\n",
"It is helpful to begin with an overview of the mechanism."
]
},
{
"cell_type": "markdown",
"id": "1f36bb40",
"metadata": {},
"source": [
"### Innovation Cycles\n",
"\n",
"As discussed above, two countries produce and trade with each other.\n",
"\n",
"In each country, firms innovate, producing new varieties of goods and, in doing so, receiving temporary monopoly power.\n",
"\n",
"Imitators follow and, after one period of monopoly, what had previously been new varieties now enter competitive production.\n",
"\n",
"Firms have incentives to innovate and produce new goods when the mass of varieties of goods currently in production is relatively low.\n",
"\n",
"In addition, there are strategic complementarities in the timing of innovation.\n",
"\n",
"Firms have incentives to innovate in the same period, so as to avoid competing with substitutes that are competitively produced.\n",
"\n",
"This leads to temporal clustering in innovations in each country.\n",
"\n",
"After a burst of innovation, the mass of goods currently in production increases.\n",
"\n",
"However, goods also become obsolete, so that not all survive from period to period.\n",
"\n",
"This mechanism generates a cycle, where the mass of varieties increases through simultaneous innovation and then falls through obsolescence."
]
},
{
"cell_type": "markdown",
"id": "edced7ff",
"metadata": {},
"source": [
"### Synchronization\n",
"\n",
"In the absence of trade, the timing of innovation cycles in each country is decoupled.\n",
"\n",
"This will be the case when trade costs are prohibitively high.\n",
"\n",
"If trade costs fall, then goods produced in each country penetrate each other’s markets.\n",
"\n",
"As illustrated below, this leads to synchronization of business cycles across the two countries."
]
},
{
"cell_type": "markdown",
"id": "e57cd0c6",
"metadata": {},
"source": [
"## Model\n",
"\n",
"Let’s write down the model more formally.\n",
"\n",
"(The treatment is relatively terse since full details can be found in [the original paper](http://www.centreformacroeconomics.ac.uk/Discussion-Papers/2015/CFMDP2015-27-Paper.pdf))\n",
"\n",
"Time is discrete with $ t = 0, 1, \\dots $.\n",
"\n",
"There are two countries indexed by $ j $ or $ k $.\n",
"\n",
"In each country, a representative household inelastically supplies $ L_j $ units of labor at wage rate $ w_{j, t} $.\n",
"\n",
"Without loss of generality, it is assumed that $ L_{1} \\geq L_{2} $.\n",
"\n",
"Households consume a single nontradeable final good which is produced competitively.\n",
"\n",
"Its production involves combining two types of tradeable intermediate inputs\n",
"via\n",
"\n",
"$$\n",
"Y_{k, t} = C_{k, t} = \\left( \\frac{X^o_{k, t}}{1 - \\alpha} \\right)^{1-\\alpha} \\left( \\frac{X_{k, t}}{\\alpha} \\right)^{\\alpha}\n",
"$$\n",
"\n",
"Here $ X^o_{k, t} $ is a homogeneous input which can be produced from labor using a linear, one-for-one technology.\n",
"\n",
"It is freely tradeable, competitively supplied, and homogeneous across countries.\n",
"\n",
"By choosing the price of this good as numeraire and assuming both countries find it optimal to always produce the homogeneous good, we can set $ w_{1, t} = w_{2, t} = 1 $.\n",
"\n",
"The good $ X_{k, t} $ is a composite, built from many differentiated goods via\n",
"\n",
"$$\n",
"X_{k, t}^{1 - \\frac{1}{\\sigma}} = \\int_{\\Omega_t} \\left[ x_{k, t}(\\nu) \\right]^{1 - \\frac{1}{\\sigma}} d \\nu\n",
"$$\n",
"\n",
"Here $ x_{k, t}(\\nu) $ is the total amount of a differentiated good $ \\nu \\in \\Omega_t $ that is produced.\n",
"\n",
"The parameter $ \\sigma > 1 $ is the direct partial elasticity of substitution between a pair of varieties and $ \\Omega_t $ is the set of varieties available in period\n",
"$ t $.\n",
"\n",
"We can split the varieties into those which are supplied competitively and those supplied monopolistically; that is, $ \\Omega_t = \\Omega_t^c + \\Omega_t^m $."
]
},
{
"cell_type": "markdown",
"id": "cf7652ba",
"metadata": {},
"source": [
"### Prices\n",
"\n",
"Demand for differentiated inputs is\n",
"\n",
"$$\n",
"x_{k, t}(\\nu) = \\left( \\frac{p_{k, t}(\\nu)}{P_{k, t}} \\right)^{-\\sigma} \\frac{\\alpha L_k}{P_{k, t}}\n",
"$$\n",
"\n",
"Here\n",
"\n",
"- $ p_{k, t}(\\nu) $ is the price of the variety $ \\nu $ and \n",
"- $ P_{k, t} $ is the price index for differentiated inputs in $ k $,\n",
" defined by \n",
"\n",
"\n",
"$$\n",
"\\left[ P_{k, t} \\right]^{1 - \\sigma} = \\int_{\\Omega_t} [p_{k, t}(\\nu) ]^{1-\\sigma} d\\nu\n",
"$$\n",
"\n",
"The price of a variety also depends on the origin, $ j $, and destination, $ k $, of the goods because shipping\n",
"varieties between countries incurs an iceberg trade cost\n",
"$ \\tau_{j,k} $.\n",
"\n",
"Thus the effective price in country $ k $ of a variety $ \\nu $ produced in country $ j $ becomes $ p_{k, t}(\\nu) = \\tau_{j,k} \\, p_{j, t}(\\nu) $.\n",
"\n",
"Using these expressions, we can derive the total demand for each variety,\n",
"which is\n",
"\n",
"$$\n",
"D_{j, t}(\\nu) = \\sum_k \\tau_{j, k} x_{k, t}(\\nu) = \\alpha A_{j, t}(p_{j, t}(\\nu))^{-\\sigma}\n",
"$$\n",
"\n",
"where\n",
"\n",
"$$\n",
"A_{j, t} := \\sum_k \\frac{\\rho_{j, k} L_{k}}{(P_{k, t})^{1 - \\sigma}}\n",
"\\quad \\text{and} \\quad\n",
"\\rho_{j, k} = (\\tau_{j, k})^{1 - \\sigma} \\leq 1\n",
"$$\n",
"\n",
"It is assumed that $ \\tau_{1,1} = \\tau_{2,2} = 1 $ and $ \\tau_{1,2} = \\tau_{2,1} = \\tau $ for some $ \\tau > 1 $, so that\n",
"\n",
"$$\n",
"\\rho_{1,2} = \\rho_{2,1} = \\rho := \\tau^{1 - \\sigma} < 1\n",
"$$\n",
"\n",
"The value $ \\rho \\in [0, 1) $ is a proxy for the degree of globalization.\n",
"\n",
"Producing one unit of each differentiated variety requires $ \\psi $ units of labor, so the marginal cost is equal to $ \\psi $ for $ \\nu \\in \\Omega_{j, t} $.\n",
"\n",
"Additionally, all competitive varieties will have the same price (because of equal marginal cost), which means that, for all $ \\nu \\in \\Omega^c $,\n",
"\n",
"$$\n",
"p_{j, t}(\\nu) = p_{j, t}^c := \\psi\n",
"\\quad \\text{and} \\quad\n",
"D_{j, t} = y_{j, t}^c := \\alpha A_{j, t} (p_{j, t}^c)^{-\\sigma}\n",
"$$\n",
"\n",
"Monopolists will have the same marked-up price, so, for all $ \\nu \\in \\Omega^m $ ,\n",
"\n",
"$$\n",
"p_{j, t}(\\nu) = p_{j, t}^m := \\frac{\\psi }{1 - \\frac{1}{\\sigma}}\n",
"\\quad \\text{and} \\quad\n",
"D_{j, t} = y_{j, t}^m := \\alpha A_{j, t} (p_{j, t}^m)^{-\\sigma}\n",
"$$\n",
"\n",
"Define\n",
"\n",
"$$\n",
"\\theta\n",
":= \\frac{p_{j, t}^c}{p_{j, t}^m} \\frac{y_{j, t}^c}{y_{j, t}^m}\n",
"= \\left(1 - \\frac{1}{\\sigma} \\right)^{1-\\sigma}\n",
"$$\n",
"\n",
"Using the preceding definitions and some algebra, the price indices can now be rewritten as\n",
"\n",
"$$\n",
"\\left(\\frac{P_{k,t}}{\\psi}\\right)^{1-\\sigma} = M_{k,t} + \\rho M_{j,t}\n",
"\\quad \\text{where} \\quad\n",
"M_{j,t} := N_{j,t}^c + \\frac{N_{j,t}^m}{ \\theta}\n",
"$$\n",
"\n",
"The symbols $ N_{j, t}^c $ and $ N_{j, t}^m $ will denote the measures of $ \\Omega^c $ and $ \\Omega^m $ respectively."
]
},
{
"cell_type": "markdown",
"id": "079d44ca",
"metadata": {},
"source": [
"### New Varieties\n",
"\n",
"To introduce a new variety, a firm must hire $ f $ units of labor per variety in each country.\n",
"\n",
"Monopolist profits must be less than or equal to zero in expectation, so\n",
"\n",
"$$\n",
"N_{j,t}^m \\geq 0, \\quad\n",
"\\pi_{j, t}^m := (p_{j, t}^m - \\psi) y_{j, t}^m - f \\leq 0\n",
"\\quad \\text{and} \\quad\n",
"\\pi_{j, t}^m N_{j,t}^m = 0\n",
"$$\n",
"\n",
"With further manipulations, this becomes\n",
"\n",
"$$\n",
"N_{j,t}^m = \\theta(M_{j,t} - N_{j,t}^c) \\geq 0,\n",
"\\quad\n",
"\\frac{1}{\\sigma}\n",
"\\left[\n",
" \\frac{\\alpha L_j}{\\theta(M_{j,t} + \\rho M_{k,t})} +\n",
" \\frac{\\alpha L_k}{\\theta(M_{j,t} + M_{k,t} / \\rho)}\n",
"\\right]\n",
"\\leq f\n",
"$$"
]
},
{
"cell_type": "markdown",
"id": "55374138",
"metadata": {},
"source": [
"### Law of Motion\n",
"\n",
"With $ \\delta $ as the exogenous probability of a variety becoming obsolete,\n",
"the dynamic equation for the measure of firms becomes\n",
"\n",
"$$\n",
"N_{j, t+1}^c = \\delta (N_{j, t}^c + N_{j, t}^m) = \\delta (N_{j, t}^c + \\theta(M_{j, t} - N_{j, t}^c))\n",
"$$\n",
"\n",
"We will work with a normalized measure of varieties\n",
"\n",
"$$\n",
"n_{j, t} := \\frac{\\theta \\sigma f N_{j, t}^c}{\\alpha (L_1 + L_2)},\n",
"\\quad\n",
"i_{j, t} := \\frac{\\theta \\sigma f N_{j, t}^m}{\\alpha (L_1 + L_2)},\n",
"\\quad\n",
"m_{j, t} := \\frac{\\theta \\sigma f M_{j, t}}{\\alpha (L_1 + L_2)} = n_{j, t} + \\frac{i_{j, t}}{\\theta}\n",
"$$\n",
"\n",
"We also use $ s_j := \\frac{L_j}{L_1 + L_2} $ to be the share of labor employed in country $ j $.\n",
"\n",
"We can use these definitions and the preceding expressions to obtain a law of\n",
"motion for $ n_t := (n_{1, t}, n_{2, t}) $.\n",
"\n",
"In particular, given an initial condition, $ n_0 = (n_{1, 0}, n_{2, 0}) \\in \\mathbb{R}_{+}^{2} $, the equilibrium trajectory, $ \\{ n_t \\}_{t=0}^{\\infty} = \\{ (n_{1, t}, n_{2, t}) \\}_{t=0}^{\\infty} $, is obtained by iterating on $ n_{t+1} = F(n_t) $ where $ F : \\mathbb{R}_{+}^{2} \\rightarrow \\mathbb{R}_{+}^{2} $ is given by\n",
"\n",
"$$\n",
"\\begin{aligned}\n",
" F(n_t)\n",
" &=\n",
" \\begin{cases}\n",
" \\big( \\delta (\\theta s_1(\\rho) + (1-\\theta) n_{1, t}), \\delta (\\theta s_2(\\rho) + (1-\\theta) n_{2, t}) \\big) \\; & \\text{for } n_t \\in D_{LL} \\\\\n",
" \\big( \\delta n_{1, t}, \\delta n_{2, t} \\big) \\; &\\text{for } n_t \\in D_{HH} \\\\\n",
" \\big( \\delta n_{1, t}, \\delta (\\theta h_2(n_{1, t}) + (1-\\theta) n_{2, t}) \\big) &\\text{for } n_t \\in D_{HL} \\\\\n",
" \\big( \\delta (\\theta h_1(n_{2, t}) + (1-\\theta) n_{1, t}, \\delta n_{2, t}) \\big) &\\text{for } n_t \\in D_{LH}\n",
" \\end{cases}\n",
"\\end{aligned}\n",
"$$\n",
"\n",
"Here\n",
"\n",
"$$\n",
"\\begin{aligned}\n",
" D_{LL} & := \\{ (n_1, n_2) \\in \\mathbb{R}_{+}^{2} | n_j \\leq s_j(\\rho) \\} \\\\\n",
" D_{HH} & := \\{ (n_1, n_2) \\in \\mathbb{R}_{+}^{2} | n_j \\geq h_j(n_k) \\} \\\\\n",
" D_{HL} & := \\{ (n_1, n_2) \\in \\mathbb{R}_{+}^{2} | n_1 \\geq s_1(\\rho) \\text{ and } n_2 \\leq h_2(n_1) \\} \\\\\n",
" D_{LH} & := \\{ (n_1, n_2) \\in \\mathbb{R}_{+}^{2} | n_1 \\leq h_1(n_2) \\text{ and } n_2 \\geq s_2(\\rho) \\}\n",
"\\end{aligned}\n",
"$$\n",
"\n",
"while\n",
"\n",
"$$\n",
"s_1(\\rho) = 1 - s_2(\\rho)\n",
"= \\min \\left\\{ \\frac{s_1 - \\rho s_2}{1 - \\rho}, 1 \\right\\}\n",
"$$\n",
"\n",
"and $ h_j(n_k) $ is defined implicitly by the equation\n",
"\n",
"$$\n",
"1 = \\frac{s_j}{h_j(n_k) + \\rho n_k} + \\frac{s_k}{h_j(n_k) + n_k / \\rho}\n",
"$$\n",
"\n",
"Rewriting the equation above gives us a quadratic equation in terms of $ h_j(n_k) $.\n",
"\n",
"Since we know $ h_j(n_k) > 0 $ then we can just solve the quadratic equation and return the positive root.\n",
"\n",
"This gives us\n",
"\n",
"$$\n",
"h_j(n_k)^2 + \\left( (\\rho + \\frac{1}{\\rho}) n_k - s_j - s_k \\right) h_j(n_k) + (n_k^2 - \\frac{s_j n_k}{\\rho} - s_k n_k \\rho) = 0\n",
"$$"
]
},
{
"cell_type": "markdown",
"id": "f641197d",
"metadata": {},
"source": [
"## Simulation\n",
"\n",
"Let’s try simulating some of these trajectories.\n",
"\n",
"We will focus in particular on whether or not innovation cycles synchronize\n",
"across the two countries.\n",
"\n",
"As we will see, this depends on initial conditions.\n",
"\n",
"For some parameterizations, synchronization will occur for “most” initial conditions, while for others synchronization will be rare.\n",
"\n",
"The computational burden of testing synchronization across many initial\n",
"conditions is not trivial.\n",
"\n",
"In order to make our code fast, we will use just in time compiled functions that will get called and handled by our class.\n",
"\n",
"These are the `@jit` statements that you see below (review [this lecture](https://python-programming.quantecon.org/numba.html) if you don’t recall how to use JIT compilation).\n",
"\n",
"Here’s the main body of code"
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "68182c7d",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"@jit(nopython=True)\n",
"def _hj(j, nk, s1, s2, θ, δ, ρ):\n",
" \"\"\"\n",
" If we expand the implicit function for h_j(n_k) then we find that\n",
" it is quadratic. We know that h_j(n_k) > 0 so we can get its\n",
" value by using the quadratic form\n",
" \"\"\"\n",
" # Find out who's h we are evaluating\n",
" if j == 1:\n",
" sj = s1\n",
" sk = s2\n",
" else:\n",
" sj = s2\n",
" sk = s1\n",
"\n",
" # Coefficients on the quadratic a x^2 + b x + c = 0\n",
" a = 1.0\n",
" b = ((ρ + 1 / ρ) * nk - sj - sk)\n",
" c = (nk * nk - (sj * nk) / ρ - sk * ρ * nk)\n",
"\n",
" # Positive solution of quadratic form\n",
" root = (-b + np.sqrt(b * b - 4 * a * c)) / (2 * a)\n",
"\n",
" return root\n",
"\n",
"@jit(nopython=True)\n",
"def DLL(n1, n2, s1_ρ, s2_ρ, s1, s2, θ, δ, ρ):\n",
" \"Determine whether (n1, n2) is in the set DLL\"\n",
" return (n1 <= s1_ρ) and (n2 <= s2_ρ)\n",
"\n",
"@jit(nopython=True)\n",
"def DHH(n1, n2, s1_ρ, s2_ρ, s1, s2, θ, δ, ρ):\n",
" \"Determine whether (n1, n2) is in the set DHH\"\n",
" return (n1 >= _hj(1, n2, s1, s2, θ, δ, ρ)) and \\\n",
" (n2 >= _hj(2, n1, s1, s2, θ, δ, ρ))\n",
"\n",
"@jit(nopython=True)\n",
"def DHL(n1, n2, s1_ρ, s2_ρ, s1, s2, θ, δ, ρ):\n",
" \"Determine whether (n1, n2) is in the set DHL\"\n",
" return (n1 >= s1_ρ) and (n2 <= _hj(2, n1, s1, s2, θ, δ, ρ))\n",
"\n",
"@jit(nopython=True)\n",
"def DLH(n1, n2, s1_ρ, s2_ρ, s1, s2, θ, δ, ρ):\n",
" \"Determine whether (n1, n2) is in the set DLH\"\n",
" return (n1 <= _hj(1, n2, s1, s2, θ, δ, ρ)) and (n2 >= s2_ρ)\n",
"\n",
"@jit(nopython=True)\n",
"def one_step(n1, n2, s1_ρ, s2_ρ, s1, s2, θ, δ, ρ):\n",
" \"\"\"\n",
" Takes a current value for (n_{1, t}, n_{2, t}) and returns the\n",
" values (n_{1, t+1}, n_{2, t+1}) according to the law of motion.\n",
" \"\"\"\n",
" # Depending on where we are, evaluate the right branch\n",
" if DLL(n1, n2, s1_ρ, s2_ρ, s1, s2, θ, δ, ρ):\n",
" n1_tp1 = δ * (θ * s1_ρ + (1 - θ) * n1)\n",
" n2_tp1 = δ * (θ * s2_ρ + (1 - θ) * n2)\n",
" elif DHH(n1, n2, s1_ρ, s2_ρ, s1, s2, θ, δ, ρ):\n",
" n1_tp1 = δ * n1\n",
" n2_tp1 = δ * n2\n",
" elif DHL(n1, n2, s1_ρ, s2_ρ, s1, s2, θ, δ, ρ):\n",
" n1_tp1 = δ * n1\n",
" n2_tp1 = δ * (θ * _hj(2, n1, s1, s2, θ, δ, ρ) + (1 - θ) * n2)\n",
" elif DLH(n1, n2, s1_ρ, s2_ρ, s1, s2, θ, δ, ρ):\n",
" n1_tp1 = δ * (θ * _hj(1, n2, s1, s2, θ, δ, ρ) + (1 - θ) * n1)\n",
" n2_tp1 = δ * n2\n",
"\n",
" return n1_tp1, n2_tp1\n",
"\n",
"@jit(nopython=True)\n",
"def n_generator(n1_0, n2_0, s1_ρ, s2_ρ, s1, s2, θ, δ, ρ):\n",
" \"\"\"\n",
" Given an initial condition, continues to yield new values of\n",
" n1 and n2\n",
" \"\"\"\n",
" n1_t, n2_t = n1_0, n2_0\n",
" while True:\n",
" n1_tp1, n2_tp1 = one_step(n1_t, n2_t, s1_ρ, s2_ρ, s1, s2, θ, δ, ρ)\n",
" yield (n1_tp1, n2_tp1)\n",
" n1_t, n2_t = n1_tp1, n2_tp1\n",
"\n",
"@jit(nopython=True)\n",
"def _pers_till_sync(n1_0, n2_0, s1_ρ, s2_ρ, s1, s2, θ, δ, ρ, maxiter, npers):\n",
" \"\"\"\n",
" Takes initial values and iterates forward to see whether\n",
" the histories eventually end up in sync.\n",
"\n",
" If countries are symmetric then as soon as the two countries have the\n",
" same measure of firms then they will be synchronized -- However, if\n",
" they are not symmetric then it is possible they have the same measure\n",
" of firms but are not yet synchronized. To address this, we check whether\n",
" firms stay synchronized for `npers` periods with Euclidean norm\n",
"\n",
" Parameters\n",
" ----------\n",
" n1_0 : scalar(Float)\n",
" Initial normalized measure of firms in country one\n",
" n2_0 : scalar(Float)\n",
" Initial normalized measure of firms in country two\n",
" maxiter : scalar(Int)\n",
" Maximum number of periods to simulate\n",
" npers : scalar(Int)\n",
" Number of periods we would like the countries to have the\n",
" same measure for\n",
"\n",
" Returns\n",
" -------\n",
" synchronized : scalar(Bool)\n",
" Did the two economies end up synchronized\n",
" pers_2_sync : scalar(Int)\n",
" The number of periods required until they synchronized\n",
" \"\"\"\n",
" # Initialize the status of synchronization\n",
" synchronized = False\n",
" pers_2_sync = maxiter\n",
" iters = 0\n",
"\n",
" # Initialize generator\n",
" n_gen = n_generator(n1_0, n2_0, s1_ρ, s2_ρ, s1, s2, θ, δ, ρ)\n",
"\n",
" # Will use a counter to determine how many times in a row\n",
" # the firm measures are the same\n",
" nsync = 0\n",
"\n",
" while (not synchronized) and (iters < maxiter):\n",
" # Increment the number of iterations and get next values\n",
" iters += 1\n",
" n1_t, n2_t = next(n_gen)\n",
"\n",
" # Check whether same in this period\n",
" if abs(n1_t - n2_t) < 1e-8:\n",
" nsync += 1\n",
" # If not, then reset the nsync counter\n",
" else:\n",
" nsync = 0\n",
"\n",
" # If we have been in sync for npers then stop and countries\n",
" # became synchronized nsync periods ago\n",
" if nsync > npers:\n",
" synchronized = True\n",
" pers_2_sync = iters - nsync\n",
"\n",
" return synchronized, pers_2_sync\n",
"\n",
"@jit(nopython=True)\n",
"def _create_attraction_basis(s1_ρ, s2_ρ, s1, s2, θ, δ, ρ,\n",
" maxiter, npers, npts):\n",
" # Create unit range with npts\n",
" synchronized, pers_2_sync = False, 0\n",
" unit_range = np.linspace(0.0, 1.0, npts)\n",
"\n",
" # Allocate space to store time to sync\n",
" time_2_sync = np.empty((npts, npts))\n",
" # Iterate over initial conditions\n",
" for (i, n1_0) in enumerate(unit_range):\n",
" for (j, n2_0) in enumerate(unit_range):\n",
" synchronized, pers_2_sync = _pers_till_sync(n1_0, n2_0, s1_ρ,\n",
" s2_ρ, s1, s2, θ, δ,\n",
" ρ, maxiter, npers)\n",
" time_2_sync[i, j] = pers_2_sync\n",
"\n",
" return time_2_sync\n",
"\n",
"\n",
"# == Now we define a class for the model == #\n",
"\n",
"class MSGSync:\n",
" \"\"\"\n",
" The paper \"Globalization and Synchronization of Innovation Cycles\" presents\n",
" a two-country model with endogenous innovation cycles. Combines elements\n",
" from Deneckere Judd (1985) and Helpman Krugman (1985) to allow for a\n",
" model with trade that has firms who can introduce new varieties into\n",
" the economy.\n",
"\n",
" We focus on being able to determine whether the two countries eventually\n",
" synchronize their innovation cycles. To do this, we only need a few\n",
" of the many parameters. In particular, we need the parameters listed\n",
" below\n",
"\n",
" Parameters\n",
" ----------\n",
" s1 : scalar(Float)\n",
" Amount of total labor in country 1 relative to total worldwide labor\n",
" θ : scalar(Float)\n",
" A measure of how much more of the competitive variety is used in\n",
" production of final goods\n",
" δ : scalar(Float)\n",
" Percentage of firms that are not exogenously destroyed every period\n",
" ρ : scalar(Float)\n",
" Measure of how expensive it is to trade between countries\n",
" \"\"\"\n",
" def __init__(self, s1=0.5, θ=2.5, δ=0.7, ρ=0.2):\n",
" # Store model parameters\n",
" self.s1, self.θ, self.δ, self.ρ = s1, θ, δ, ρ\n",
"\n",
" # Store other cutoffs and parameters we use\n",
" self.s2 = 1 - s1\n",
" self.s1_ρ = self._calc_s1_ρ()\n",
" self.s2_ρ = 1 - self.s1_ρ\n",
"\n",
" def _unpack_params(self):\n",
" return self.s1, self.s2, self.θ, self.δ, self.ρ\n",
"\n",
" def _calc_s1_ρ(self):\n",
" # Unpack params\n",
" s1, s2, θ, δ, ρ = self._unpack_params()\n",
"\n",
" # s_1(ρ) = min(val, 1)\n",
" val = (s1 - ρ * s2) / (1 - ρ)\n",
" return min(val, 1)\n",
"\n",
" def simulate_n(self, n1_0, n2_0, T):\n",
" \"\"\"\n",
" Simulates the values of (n1, n2) for T periods\n",
"\n",
" Parameters\n",
" ----------\n",
" n1_0 : scalar(Float)\n",
" Initial normalized measure of firms in country one\n",
" n2_0 : scalar(Float)\n",
" Initial normalized measure of firms in country two\n",
" T : scalar(Int)\n",
" Number of periods to simulate\n",
"\n",
" Returns\n",
" -------\n",
" n1 : Array(Float64, ndim=1)\n",
" A history of normalized measures of firms in country one\n",
" n2 : Array(Float64, ndim=1)\n",
" A history of normalized measures of firms in country two\n",
" \"\"\"\n",
" # Unpack parameters\n",
" s1, s2, θ, δ, ρ = self._unpack_params()\n",
" s1_ρ, s2_ρ = self.s1_ρ, self.s2_ρ\n",
"\n",
" # Allocate space\n",
" n1 = np.empty(T)\n",
" n2 = np.empty(T)\n",
"\n",
" # Create the generator\n",
" n1[0], n2[0] = n1_0, n2_0\n",
" n_gen = n_generator(n1_0, n2_0, s1_ρ, s2_ρ, s1, s2, θ, δ, ρ)\n",
"\n",
" # Simulate for T periods\n",
" for t in range(1, T):\n",
" # Get next values\n",
" n1_tp1, n2_tp1 = next(n_gen)\n",
"\n",
" # Store in arrays\n",
" n1[t] = n1_tp1\n",
" n2[t] = n2_tp1\n",
"\n",
" return n1, n2\n",
"\n",
" def pers_till_sync(self, n1_0, n2_0, maxiter=500, npers=3):\n",
" \"\"\"\n",
" Takes initial values and iterates forward to see whether\n",
" the histories eventually end up in sync.\n",
"\n",
" If countries are symmetric then as soon as the two countries have the\n",
" same measure of firms then they will be synchronized -- However, if\n",
" they are not symmetric then it is possible they have the same measure\n",
" of firms but are not yet synchronized. To address this, we check whether\n",
" firms stay synchronized for `npers` periods with Euclidean norm\n",
"\n",
" Parameters\n",
" ----------\n",
" n1_0 : scalar(Float)\n",
" Initial normalized measure of firms in country one\n",
" n2_0 : scalar(Float)\n",
" Initial normalized measure of firms in country two\n",
" maxiter : scalar(Int)\n",
" Maximum number of periods to simulate\n",
" npers : scalar(Int)\n",
" Number of periods we would like the countries to have the\n",
" same measure for\n",
"\n",
" Returns\n",
" -------\n",
" synchronized : scalar(Bool)\n",
" Did the two economies end up synchronized\n",
" pers_2_sync : scalar(Int)\n",
" The number of periods required until they synchronized\n",
" \"\"\"\n",
" # Unpack parameters\n",
" s1, s2, θ, δ, ρ = self._unpack_params()\n",
" s1_ρ, s2_ρ = self.s1_ρ, self.s2_ρ\n",
"\n",
" return _pers_till_sync(n1_0, n2_0, s1_ρ, s2_ρ,\n",
" s1, s2, θ, δ, ρ, maxiter, npers)\n",
"\n",
" def create_attraction_basis(self, maxiter=250, npers=3, npts=50):\n",
" \"\"\"\n",
" Creates an attraction basis for values of n on [0, 1] X [0, 1]\n",
" with npts in each dimension\n",
" \"\"\"\n",
" # Unpack parameters\n",
" s1, s2, θ, δ, ρ = self._unpack_params()\n",
" s1_ρ, s2_ρ = self.s1_ρ, self.s2_ρ\n",
"\n",
" ab = _create_attraction_basis(s1_ρ, s2_ρ, s1, s2, θ, δ,\n",
" ρ, maxiter, npers, npts)\n",
"\n",
" return ab"
]
},
{
"cell_type": "markdown",
"id": "eb4717e5",
"metadata": {},
"source": [
"### Time Series of Firm Measures\n",
"\n",
"We write a short function below that exploits the preceding code and plots two time series.\n",
"\n",
"Each time series gives the dynamics for the two countries.\n",
"\n",
"The time series share parameters but differ in their initial condition.\n",
"\n",
"Here’s the function"
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "600a951b",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"def plot_timeseries(n1_0, n2_0, s1=0.5, θ=2.5,\n",
" δ=0.7, ρ=0.2, ax=None, title=''):\n",
" \"\"\"\n",
" Plot a single time series with initial conditions\n",
" \"\"\"\n",
" if ax is None:\n",
" fig, ax = plt.subplots()\n",
"\n",
" # Create the MSG Model and simulate with initial conditions\n",
" model = MSGSync(s1, θ, δ, ρ)\n",
" n1, n2 = model.simulate_n(n1_0, n2_0, 25)\n",
"\n",
" ax.plot(np.arange(25), n1, label=\"$n_1$\", lw=2)\n",
" ax.plot(np.arange(25), n2, label=\"$n_2$\", lw=2)\n",
"\n",
" ax.legend()\n",
" ax.set(title=title, ylim=(0.15, 0.8))\n",
"\n",
" return ax\n",
"\n",
"\n",
"# Create figure\n",
"fig, ax = plt.subplots(2, 1, figsize=(10, 8))\n",
"\n",
"plot_timeseries(0.15, 0.35, ax=ax[0], title='Not Synchronized')\n",
"plot_timeseries(0.4, 0.3, ax=ax[1], title='Synchronized')\n",
"\n",
"fig.tight_layout()\n",
"\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"id": "82ab639e",
"metadata": {},
"source": [
"In the first case, innovation in the two countries does not synchronize.\n",
"\n",
"In the second case, different initial conditions are chosen, and the cycles\n",
"become synchronized."
]
},
{
"cell_type": "markdown",
"id": "34c7f08e",
"metadata": {},
"source": [
"### Basin of Attraction\n",
"\n",
"Next, let’s study the initial conditions that lead to synchronized cycles more\n",
"systematically.\n",
"\n",
"We generate time series from a large collection of different initial\n",
"conditions and mark those conditions with different colors according to\n",
"whether synchronization occurs or not.\n",
"\n",
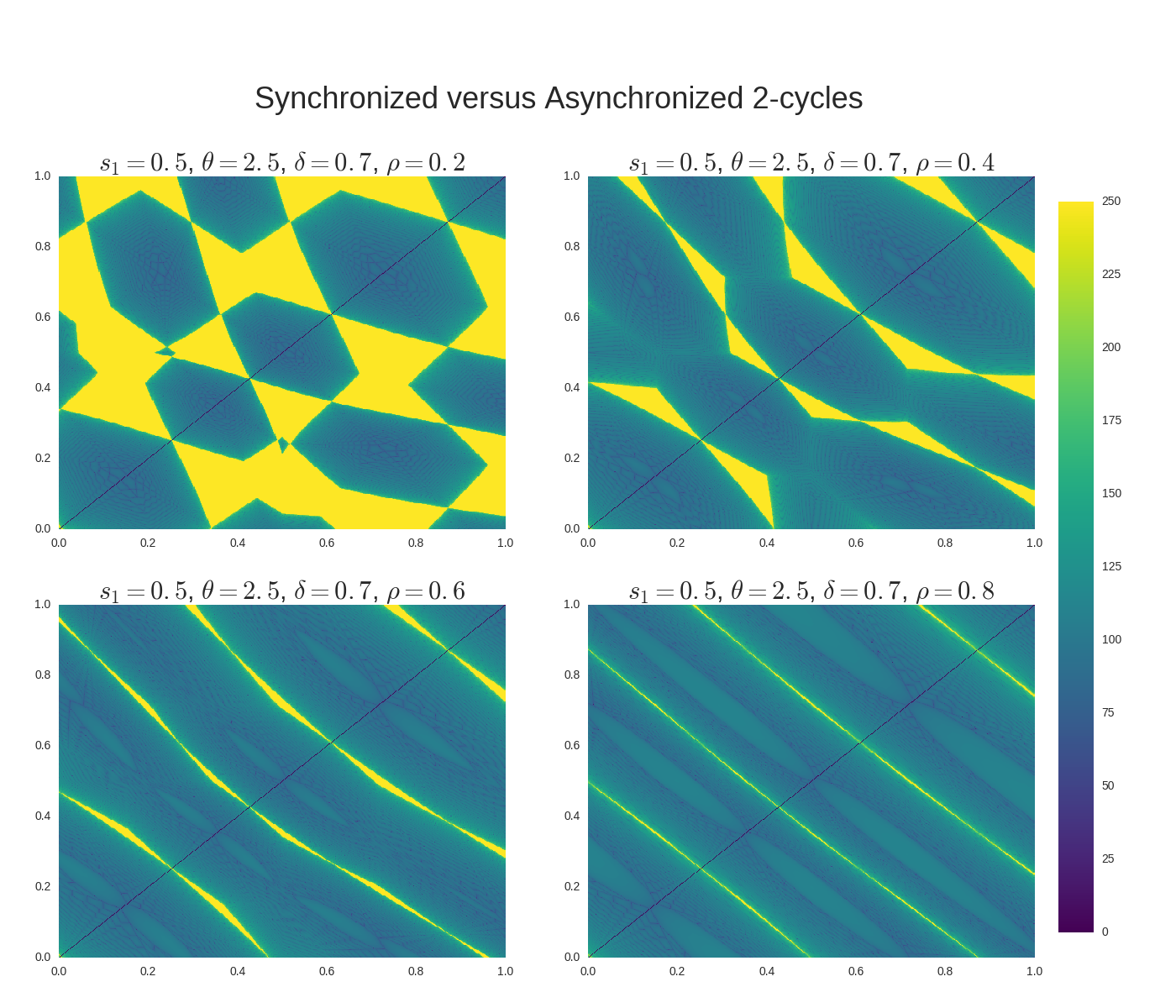
"The next display shows exactly this for four different parameterizations (one\n",
"for each subfigure).\n",
"\n",
"Dark colors indicate synchronization, while light colors indicate failure to synchronize.\n",
"\n",
"\n",
"\n",
"\n",
"\n",
" \n",
"As you can see, larger values of $ \\rho $ translate to more synchronization.\n",
"\n",
"You are asked to replicate this figure in the exercises.\n",
"\n",
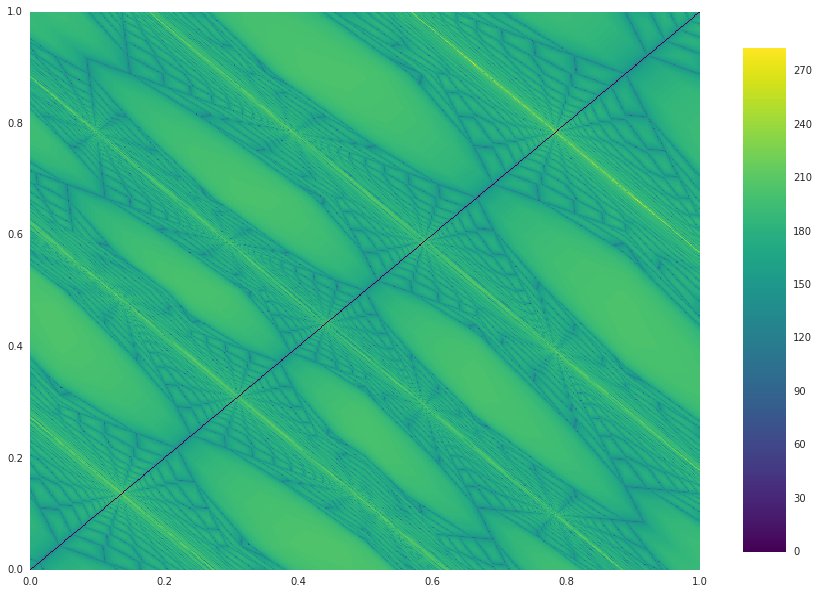
"In the solution to the exercises, you’ll also find a figure with sliders, allowing you to experiment with different parameters.\n",
"\n",
"Here’s one snapshot from the interactive figure\n",
"\n",
""
]
},
{
"cell_type": "markdown",
"id": "75ca620e",
"metadata": {},
"source": [
"## Exercises"
]
},
{
"cell_type": "markdown",
"id": "44639782",
"metadata": {},
"source": [
"## Exercise 14.1\n",
"\n",
"Replicate the figure [shown above](#matsrep) by coloring initial conditions according to whether or not synchronization occurs from those conditions."
]
},
{
"cell_type": "markdown",
"id": "85edaac0",
"metadata": {},
"source": [
"## Solution to[ Exercise 14.1](https://python-advanced.quantecon.org/#matsuyama_ex1)"
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "5bc0558a",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"def plot_attraction_basis(s1=0.5, θ=2.5, δ=0.7, ρ=0.2, npts=250, ax=None):\n",
" if ax is None:\n",
" fig, ax = plt.subplots()\n",
"\n",
" # Create attraction basis\n",
" unitrange = np.linspace(0, 1, npts)\n",
" model = MSGSync(s1, θ, δ, ρ)\n",
" ab = model.create_attraction_basis(npts=npts)\n",
" cf = ax.pcolormesh(unitrange, unitrange, ab, cmap=\"viridis\")\n",
"\n",
" return ab, cf\n",
"\n",
"\n",
"fig = plt.figure(figsize=(14, 12))\n",
"\n",
"# Left - Bottom - Width - Height\n",
"ax0 = fig.add_axes((0.05, 0.475, 0.38, 0.35), label=\"axes0\")\n",
"ax1 = fig.add_axes((0.5, 0.475, 0.38, 0.35), label=\"axes1\")\n",
"ax2 = fig.add_axes((0.05, 0.05, 0.38, 0.35), label=\"axes2\")\n",
"ax3 = fig.add_axes((0.5, 0.05, 0.38, 0.35), label=\"axes3\")\n",
"\n",
"params = [[0.5, 2.5, 0.7, 0.2],\n",
" [0.5, 2.5, 0.7, 0.4],\n",
" [0.5, 2.5, 0.7, 0.6],\n",
" [0.5, 2.5, 0.7, 0.8]]\n",
"\n",
"ab0, cf0 = plot_attraction_basis(*params[0], npts=500, ax=ax0)\n",
"ab1, cf1 = plot_attraction_basis(*params[1], npts=500, ax=ax1)\n",
"ab2, cf2 = plot_attraction_basis(*params[2], npts=500, ax=ax2)\n",
"ab3, cf3 = plot_attraction_basis(*params[3], npts=500, ax=ax3)\n",
"\n",
"cbar_ax = fig.add_axes([0.9, 0.075, 0.03, 0.725])\n",
"plt.colorbar(cf0, cax=cbar_ax)\n",
"\n",
"ax0.set_title(r\"$s_1=0.5$, $\\theta=2.5$, $\\delta=0.7$, $\\rho=0.2$\",\n",
" fontsize=22)\n",
"ax1.set_title(r\"$s_1=0.5$, $\\theta=2.5$, $\\delta=0.7$, $\\rho=0.4$\",\n",
" fontsize=22)\n",
"ax2.set_title(r\"$s_1=0.5$, $\\theta=2.5$, $\\delta=0.7$, $\\rho=0.6$\",\n",
" fontsize=22)\n",
"ax3.set_title(r\"$s_1=0.5$, $\\theta=2.5$, $\\delta=0.7$, $\\rho=0.8$\",\n",
" fontsize=22)\n",
"\n",
"fig.suptitle(\"Synchronized versus Asynchronized 2-cycles\",\n",
" x=0.475, y=0.915, size=26)\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"id": "b8bc1945",
"metadata": {},
"source": [
"Additionally, instead of just seeing 4 plots at once, we might want to\n",
"manually be able to change $ \\rho $ and see how it affects the plot\n",
"in real-time. Below we use an interactive plot to do this.\n",
"\n",
"Note, interactive plotting requires the [ipywidgets](https://github.com/jupyter-widgets/ipywidgets) module to be installed and enabled."
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "60511d6a",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"def interact_attraction_basis(ρ=0.2, maxiter=250, npts=250):\n",
" # Create the figure and axis that we will plot on\n",
" fig, ax = plt.subplots(figsize=(12, 10))\n",
"\n",
" # Create model and attraction basis\n",
" s1, θ, δ = 0.5, 2.5, 0.75\n",
" model = MSGSync(s1, θ, δ, ρ)\n",
" ab = model.create_attraction_basis(maxiter=maxiter, npts=npts)\n",
"\n",
" # Color map with colormesh\n",
" unitrange = np.linspace(0, 1, npts)\n",
" cf = ax.pcolormesh(unitrange, unitrange, ab, cmap=\"viridis\")\n",
" cbar_ax = fig.add_axes([0.95, 0.15, 0.05, 0.7])\n",
" plt.colorbar(cf, cax=cbar_ax)\n",
" plt.show()\n",
" return None"
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "3b4c1b25",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"fig = interact(interact_attraction_basis,\n",
" ρ=(0.0, 1.0, 0.05),\n",
" maxiter=(50, 5000, 50),\n",
" npts=(25, 750, 25))"
]
}
],
"metadata": {
"date": 1730717050.8825865,
"filename": "matsuyama.md",
"kernelspec": {
"display_name": "Python",
"language": "python3",
"name": "python3"
},
"title": "Globalization and Cycles"
},
"nbformat": 4,
"nbformat_minor": 5
}