37. Irrelevance of Capital Structures with Complete Markets#
In addition to what’s in Anaconda, this lecture will need the following libraries:
!pip install --upgrade quantecon
!conda install -y -c plotly plotly plotly-orca
Show code cell output
Collecting quantecon
Downloading quantecon-0.7.2-py3-none-any.whl.metadata (4.9 kB)
Requirement already satisfied: numba>=0.49.0 in /home/runner/miniconda3/envs/quantecon/lib/python3.11/site-packages (from quantecon) (0.59.0)
Requirement already satisfied: numpy>=1.17.0 in /home/runner/miniconda3/envs/quantecon/lib/python3.11/site-packages (from quantecon) (1.26.4)
Requirement already satisfied: requests in /home/runner/miniconda3/envs/quantecon/lib/python3.11/site-packages (from quantecon) (2.31.0)
Requirement already satisfied: scipy>=1.5.0 in /home/runner/miniconda3/envs/quantecon/lib/python3.11/site-packages (from quantecon) (1.11.4)
Requirement already satisfied: sympy in /home/runner/miniconda3/envs/quantecon/lib/python3.11/site-packages (from quantecon) (1.12)
Requirement already satisfied: llvmlite<0.43,>=0.42.0dev0 in /home/runner/miniconda3/envs/quantecon/lib/python3.11/site-packages (from numba>=0.49.0->quantecon) (0.42.0)
Requirement already satisfied: charset-normalizer<4,>=2 in /home/runner/miniconda3/envs/quantecon/lib/python3.11/site-packages (from requests->quantecon) (2.0.4)
Requirement already satisfied: idna<4,>=2.5 in /home/runner/miniconda3/envs/quantecon/lib/python3.11/site-packages (from requests->quantecon) (3.4)
Requirement already satisfied: urllib3<3,>=1.21.1 in /home/runner/miniconda3/envs/quantecon/lib/python3.11/site-packages (from requests->quantecon) (2.0.7)
Requirement already satisfied: certifi>=2017.4.17 in /home/runner/miniconda3/envs/quantecon/lib/python3.11/site-packages (from requests->quantecon) (2024.2.2)
Requirement already satisfied: mpmath>=0.19 in /home/runner/miniconda3/envs/quantecon/lib/python3.11/site-packages (from sympy->quantecon) (1.3.0)
Downloading quantecon-0.7.2-py3-none-any.whl (215 kB)
?25l ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 0.0/215.4 kB ? eta -:--:--
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 215.4/215.4 kB 15.4 MB/s eta 0:00:00
?25h
Installing collected packages: quantecon
Successfully installed quantecon-0.7.2
Channels:
- plotly
- default
- defaults
Platform: linux-64
Collecting package metadata (repodata.json): -
\
|
/
-
\
|
/
-
\
|
/
-
\
|
/
-
\
done
Solving environment: /
-
\
|
/
-
\
|
/
-
\
|
done
## Package Plan ##
environment location: /home/runner/miniconda3/envs/quantecon
added / updated specs:
- plotly
- plotly-orca
The following packages will be downloaded:
package | build
---------------------------|-----------------
plotly-orca-1.3.1 | 1 56.6 MB plotly
------------------------------------------------------------
Total: 56.6 MB
The following NEW packages will be INSTALLED:
plotly-orca plotly/linux-64::plotly-orca-1.3.1-1
Downloading and Extracting Packages:
plotly-orca-1.3.1 | 56.6 MB | | 0%
plotly-orca-1.3.1 | 56.6 MB | ##################################### | 100%
plotly-orca-1.3.1 | 56.6 MB | ##################################### | 100%
Preparing transaction: -
done
Verifying transaction: |
/
done
Executing transaction: \
|
done
37.1. Introduction#
This is a prolegomenon to another lecture Equilibrium Capital Structures with Incomplete Markets about a model with incomplete markets authored by Bisin, Clementi, and Gottardi [Bisin et al., 2018].
We adopt specifications of preferences and technologies very close to Bisin, Clemente, and Gottardi’s but unlike them assume that there are complete markets in one-period Arrow securities.
This simplification of BCG’s setup helps us by
creating a benchmark economy to compare with outcomes in BCG’s incomplete markets economy
creating a good guess for initial values of some equilibrium objects to be computed in BCG’s incomplete markets economy via an iterative algorithm
illustrating classic complete markets outcomes that include
indeterminacy of consumers’ portfolio choices
indeterminacy of firms’ financial structures that underlies a Modigliani-Miller theorem [Modigliani and Miller, 1958]
introducing
Big K, little kissues in a simple context that will recur in the BCG incomplete markets environment
A Big K, little k analysis also played roles in this quantecon lecture as well as here and here.
37.1.1. Setup#
The economy lasts for two periods, \(t=0, 1\).
There are two types of consumers named \(i=1,2\).
A scalar random variable \(\epsilon\) with probability density \(g(\epsilon)\) affects both
the return in period \(1\) from investing \(k \geq 0\) in physical capital in period \(0\).
exogenous period \(1\) endowments of the consumption good for agents of types \(i =1\) and \(i=2\).
Type \(i=1\) and \(i=2\) agents’ period \(1\) endowments are correlated with the return on physical capital in different ways.
We discuss two arrangements:
a command economy in which a benevolent planner chooses \(k\) and allocates goods to the two types of consumers in each period and each random second period state
a competitive equilibrium with markets in claims on physical capital and a complete set (possibly a continuum) of one-period Arrow securities that pay period \(1\) consumption goods contingent on the realization of random variable \(\epsilon\).
37.1.2. Endowments#
There is a single consumption good in period \(0\) and at each random state \(\epsilon\) in period \(1\).
Economy-wide endowments in periods \(0\) and \(1\) are
Soon we’ll explain how aggregate endowments are divided between type \(i=1\) and type \(i=2\) consumers.
We don’t need to do that in order to describe a social planning problem.
37.1.3. Technology:#
Where \(\alpha \in (0,1)\) and \(A >0\)
37.1.4. Preferences:#
A consumer of type \(i\) orders period \(0\) consumption \(c_0^i\) and state \(\epsilon\), period \(1\) consumption \(c^i_1(\epsilon)\) by
\(\beta \in (0,1)\) and the one-period utility function is
37.1.5. Parameterizations#
Following BCG, we shall employ the following parameterizations:
Sometimes instead of asuming \(\epsilon \sim g(\epsilon) = {\mathcal N}(0,\sigma^2)\), we’ll assume that \(g(\cdot)\) is a probability mass function that serves as a discrete approximation to a standardized normal density.
37.1.6. Pareto criterion and planning problem#
The planner’s objective function is
where \(\phi_i \geq 0\) is a Pareto weight that the planner attaches to a consumer of type \(i\).
We form the following Lagrangian for the planner’s problem:
First-order necessary optimality conditions for the planning problem are:
The first four equations imply that
These together with the fifth first-order condition for the planner imply the following equation that determines an optimal choice of capital
for \(i = 1,2\).
37.1.7. Helpful observations and bookkeeping#
Evidently,
and
where it is to be understood that this equation holds for \(c^1 = c^1_0\) and \(c^2 = c^2_0\) and also for \(c^1 = c^1(\epsilon)\) and \(c^2 = c^2(\epsilon)\) for all \(\epsilon\).
With the same understanding, it follows that
Let \(c= c^1 + c^2\).
It follows from the preceding equation that
where \(\eta \in [0,1]\) is a function of \(\phi_1\) and \(\gamma\).
Consequently, we can write the planner’s first-order condition for \(k\) as
which is one equation to be solved for \(k \geq 0\).
Anticipating a Big K, little k idea widely used in macroeconomics,
to be discussed in detail below, let \(K\) be the value of \(k\)
that solves the preceding equation so that
The associated optimal consumption allocation is
where \(\eta \in [0,1]\) is the consumption share parameter mentioned above that is a function of the Pareto weight \(\phi_1\) and the utility curvature parameter \(\gamma\).
37.1.7.1. Remarks#
The relative Pareto weight parameter \(\eta\) does not appear in equation (37.1) that determines \(K\).
Neither does it influence \(C_0\) or \(C_1(\epsilon)\), which depend solely on \(K\).
The role of \(\eta\) is to determine how to allocate total consumption between the two types of consumers.
Thus, the planner’s choice of \(K\) does not interact with how it wants to allocate consumption.
37.2. Competitive equilibrium#
We now describe a competitive equilibrium for an economy that has specifications of consumer preferences, technology, and aggregate endowments that are identical to those in the preceding planning problem.
While prices do not appear in the planning problem – only quantities do – prices play an important role in a competitive equilibrium.
To understand how the planning economy is related to a competitive
equilibrium, we now turn to the Big K, little k distinction.
37.2.1. Measures of agents and firms#
We follow BCG in assuming that there are unit measures of
consumers of type \(i=1\)
consumers of type \(i=2\)
firms with access to the production technology that converts \(k\) units of time \(0\) good into \(A k^\alpha e^\epsilon\) units of the time \(1\) good in random state \(\epsilon\)
Thus, let \(\omega \in [0,1]\) index a particular consumer of type \(i\).
Then define Big \(C^i\) as
In the same spirit, let \(\zeta \in [0,1]\) index a particular firm. Then define Big \(K\) as
The assumption that there are continua of our three types of agents plays an important role making each individual agent into a powerless price taker:
an individual consumer chooses its own (infinesimal) part \(c^i(\omega)\) of \(C^i\) taking prices as given
an individual firm chooses its own (infinitesmimal) part \(k(\zeta)\) of \(K\) taking prices as
equilibrium prices depend on the
Big K, Big Cobjects \(K\) and \(C\)
Nevertheless, in equilibrium, \(K = k, C^i = c^i\)
The assumption about measures of agents is thus a powerful device for making a host of competitive agents take as given equilibrium prices that are determined by the independent decisions of hosts of agents who behave just like they do.
37.2.1.1. Ownership#
Consumers of type \(i\) own the following exogenous quantities of the consumption good in periods \(0\) and \(1\):
where
Consumers also own shares in a firm that operates the technology for converting nonnegative amounts of the time \(0\) consumption good one-for-one into a capital good \(k\) that produces \(A k^\alpha e^\epsilon\) units of the time \(1\) consumption good in time \(1\) state \(\epsilon\).
Consumers of types \(i=1,2\) are endowed with \(\theta_0^i\) shares of a firm and
37.2.1.2. Asset markets#
At time \(0\), consumers trade the following assets with other consumers and with firms:
equities (also known as stocks) issued by firms
one-period Arrow securities that pay one unit of consumption at time \(1\) when the shock \(\epsilon\) assumes a particular value
Later, we’ll allow the firm to issue bonds too, but not now.
37.2.2. Objects appearing in a competitive equilibrium#
Let
\(a^i(\epsilon)\) be consumer \(i\) ’s purchases of claims on time \(1\) consumption in state \(\epsilon\)
\(q(\epsilon)\) be a pricing kernel for one-period Arrow securities
\(\theta_0^i \geq 0\) be consumer \(i\)’s intial share of the firm, \(\sum_i \theta_0^i =1\)
\(\theta^i\) be the fraction of a firm’s shares purchased by consumer \(i\) at time \(t=0\)
\(V\) be the value of the representative firm
\(\tilde V\) be the value of equity issued by the representative firm
\(K, C_0\) be two scalars and \(C_1(\epsilon)\) a function that we use to construct a guess about an equilibrium pricing kernel for Arrow securities
We proceed to describe constrained optimum problems faced by consumers and a representative firm in a competitive equilibrium.
37.2.3. A representative firm’s problem#
A representative firm takes Arrow security prices \(q(\epsilon)\) as given.
The firm purchases capital \(k \geq 0\) from consumers at time \(0\) and finances itself by issuing equity at time \(0\).
The firm produces time \(1\) goods \(A k^\alpha e^\epsilon\) in
state \(\epsilon\) and pays all of these earnings to owners of its
equity.
The value of a firm’s equity at time \(0\) can be computed by multiplying its state-contingent earnings by their Arrow securities prices and then adding over all contingencies:
Owners of a firm want it to choose \(k\) to maximize
The firm’s first-order necessary condition for an optimal \(k\) is
The time \(0\) value of a representative firm is
The right side equals the value of equity minus the cost of the time \(0\) goods that it purchases and uses as capital.
37.2.4. A consumer’s problem#
We now pose a consumer’s problem in a competitive equilibrium.
As a price taker, each consumer faces a given Arrow securities pricing kernel \(q(\epsilon)\), a given value of a firm \(V\) that has chosen capital stock \(k\), a price of equity \(\tilde V\), and prospective next period random dividends \(A k^\alpha e^\epsilon\).
If we evaluate consumer \(i\)’s time \(1\) budget constraint at zero consumption \(c^i_1(\epsilon) = 0\) and solve for \(-a^i(\epsilon)\) we obtain
The quantity \(- \bar a^i(\epsilon;\theta^i)\) is the maximum amount that it is feasible for consumer \(i\) to repay to his Arrow security creditors at time \(1\) in state \(\epsilon\).
Notice that \(-\bar a^i(\epsilon;\theta^i)\) defined in (37.2) depends on
his endowment \(w_1^i(\epsilon)\) at time \(1\) in state \(\epsilon\)
his share \(\theta^i\) of a representive firm’s dividends
These constitute two sources of collateral that back the consumer’s issues of Arrow securities that pay off in state \(\epsilon\)
Consumer \(i\) chooses a scalar \(c_0^i\) and a function \(c_1^i(\epsilon)\) to maximize
subject to time \(0\) and time \(1\) budget constraints
Attach Lagrange multiplier \(\lambda_0^i\) to the budget constraint at time \(0\) and scaled Lagrange multiplier \(\beta \lambda_1^i(\epsilon) g(\epsilon)\) to the budget constraint at time \(1\) and state \(\epsilon\), then form the Lagrangian
Off corners, first-order necessary conditions for an optimum with respect to \(c_0^i, c_1^i(\epsilon),\) and \(a^i(\epsilon)\) are
These equations imply that consumer \(i\) adjusts its consumption plan to satisfy
To deduce a restriction on equilibrium prices, we solve the period \(1\) budget constraint to express \(a^i(\epsilon)\) as
then substitute the expression on the right side into the time \(0\) budget constraint and rearrange to get the single intertemporal budget constraint
The right side of inequality (37.4) is the present value of consumer \(i\)’s consumption while the left side is the present value of consumer \(i\)’s endowment when consumer \(i\) buys \(\theta^i\) shares of equity.
From inequality (37.4), we deduce two findings.
1. No arbitrage profits condition:
Unless
an arbitrage opportunity would be open.
If
the consumer could afford an arbitrarily high present value of consumption by setting \(\theta^i\) to an arbitrarily large negative number.
If
the consumer could afford an arbitrarily high present value of consumption by setting \(\theta^i\) to be arbitrarily large positive number.
Since resources are finite, there can exist no such arbitrage opportunity in a competitive equilibrium.
Therefore, it must be true that the following no arbitrage condition prevails:
Equation (37.6) asserts that the value of equity equals the value of the state-contingent dividends \(Ak^\alpha e^\epsilon\) evaluated at the Arrow security prices \(q(\epsilon; K)\) that we have expressed as a function of \(K\).
We’ll say more about this equation later.
2. Indeterminacy of portfolio
When the no-arbitrage pricing equation (37.6) prevails, a consumer of type \(i\)’s choice \(\theta^i\) of equity is indeterminate.
Consumer of type \(i\) can offset any choice of \(\theta^i\) by setting an appropriate schedule \(a^i(\epsilon)\) for purchasing state-contingent securities.
37.2.5. Computing competitive equilibrium prices and quantities#
Having computed an allocation that solves the planning problem, we can
readily compute a competitive equilibrium via the following steps that,
as we’ll see, relies heavily on the Big K, little k,
Big C, little c logic mentioned earlier:
a competitive equilbrium allocation equals the allocation chosen by the planner
competitive equilibrium prices and the value of a firm’s equity are encoded in shadow prices from the planning problem that depend on Big \(K\) and Big \(C\).
To substantiate that this procedure is valid, we proceed as follows.
With \(K\) in hand, we make the following guess for competitive equilibrium Arrow securities prices
To confirm the guess, we begin by considering its consequences for the firm’s choice of \(k\).
With Arrow securities prices (37.7), the firm’s first-order necessary condition for choosing \(k\) becomes
which can be verified to be satisfied if the firm sets
because by setting \(k=K\) equation (37.8) becomes equivalent with the planner’s first-order condition (37.1) for setting \(K\).
To pose a consumer’s problem in a competitive equilibrium, we require not only the above guess for the Arrow securities pricing kernel \(q(\epsilon)\) but the value of equity \(\tilde V\):
Let \(\tilde V\) be the value of equity implied by Arrow securities price function (37.7) and formula (37.9).
At the Arrow securities prices \(q(\epsilon)\) given by (37.7) and equity value \(\tilde V\) given by (37.9), consumer \(i=1,2\) choose consumption allocations and portolios that satisfy the first-order necessary conditions
It can be verified directly that the following choices satisfy these equations
for an \(\eta \in (0,1)\) that depends on consumers’ endowments \([w_0^1, w_0^2, w_1^1(\epsilon), w_1^2(\epsilon), \theta_0^1, \theta_0^2 ]\).
Remark: Multiple arrangements of endowments \([w_0^1, w_0^2, w_1^1(\epsilon), w_1^2(\epsilon), \theta_0^1, \theta_0^2 ]\) associated with the same distribution of wealth \(\eta\). Can you explain why?
Hint
Think about the portfolio indeterminacy finding above.
37.2.6. Modigliani-Miller theorem#
We now allow a firm to issue both bonds and equity.
Payouts from equity and bonds, respectively, are
Thus, one unit of the bond pays one unit of consumption at time \(1\) in state \(\epsilon\) if \(A k^\alpha e^\epsilon - b \geq 0\), which is true when \(\epsilon \geq \epsilon^* = \log \frac{b}{Ak^\alpha}\), and pays \(\frac{A k^\alpha e^\epsilon}{b}\) units of time \(1\) consumption in state \(\epsilon\) when \(\epsilon < \epsilon^*\).
The value of the firm is now the sum of equity plus the value of bonds, which we denote
where \(p(k,b)\) is the price of one unit of the bond when a firm with \(k\) units of physical capital issues \(b\) bonds.
We continue to assume that there are complete markets in Arrow securities with pricing kernel \(q(\epsilon)\).
A version of the no-arbitrage-in-equilibrium argument that we presented earlier implies that the value of equity and the price of bonds are
Consequently, the value of the firm is
which is the same expression that we obtained above when we assumed that the firm issued only equity.
We thus obtain a version of the celebrated Modigliani-Miller theorem [Modigliani and Miller, 1958] about firms’ finance:
Modigliani-Miller theorem:
The value of a firm is independent the mix of equity and bonds that it uses to finance its physical capital.
The firms’s decision about how much physical capital to purchase does not depend on whether it finances those purchases by issuing bonds or equity
The firm’s choice of whether to finance itself by issuing equity or bonds is indeterminant
Please note the role of the assumption of complete markets in Arrow securities in substantiating these claims.
In Equilibrium Capital Structures with Incomplete Markets, we will assume that markets are (very) incomplete – we’ll shut down markets in almost all Arrow securities.
That will pull the rug from underneath the Modigliani-Miller theorem.
37.3. Code#
We create a class object BCG_complete_markets to compute
equilibrium allocations of the complete market BCG model given a list
of parameter values.
It consists of 4 functions that do the following things:
opt_kcomputes the planner’s optimal capital \(K\)First, create a grid for capital.
Then for each value of capital stock in the grid, compute the left side of the planner’s first-order necessary condition for \(k\), that is,
\[ \beta \alpha A K^{\alpha -1} \int \left( \frac{w_1(\epsilon) + A K^\alpha e^\epsilon}{w_0 - K } \right)^{-\gamma} e^\epsilon g(\epsilon) d \epsilon - 1 =0 \]Find \(k\) that solves this equation.
qcomputes Arrow security prices as a function of the productivity shock \(\epsilon\) and capital \(K\):\[ q(\epsilon;K) = \beta \left( \frac{u'\left( w_1(\epsilon) + A K^\alpha e^\epsilon\right)} {u'(w_0 - K )} \right) \]Vsolves for the firm value given capital \(k\):\[ V = - k + \int A k^\alpha e^\epsilon q(\epsilon; K) d \epsilon \]opt_ccomputes optimal consumptions \(c^i_0\), and \(c^i(\epsilon)\):The function first computes weight \(\eta\) using the budget constraint for agent 1:
\[ w_0^1 + \theta_0^1 V + \int w_1^1(\epsilon) q(\epsilon) d \epsilon = c_0^1 + \int c_1^1(\epsilon) q(\epsilon) d \epsilon = \eta \left( C_0 + \int C_1(\epsilon) q(\epsilon) d \epsilon \right) \]where
\[ \begin{aligned} C_0 & = w_0 - K \cr C_1(\epsilon) & = w_1(\epsilon) + A K^\alpha e^\epsilon \cr \end{aligned} \]It computes consumption for each agent as
\[ \begin{aligned} c_0^1 & = \eta C_0 \cr c_0^2 & = (1 - \eta) C_0 \cr c_1^1(\epsilon) & = \eta C_1 (\epsilon) \cr c_1^2 (\epsilon) & = (1 - \eta) C_1(\epsilon) \end{aligned} \]
The list of parameters includes:
\(\chi_1\), \(\chi_2\): Correlation parameters for agents 1 and 2. Default values are 0 and 0.9, respectively.
\(w^1_0\), \(w^2_0\): Initial endowments. Default values are 1.
\(\theta^1_0\), \(\theta^2_0\): Consumers’ initial shares of a representative firm. Default values are 0.5.
\(\psi\): CRRA risk parameter. Default value is 3.
\(\alpha\): Returns to scale production function parameter. Default value is 0.6.
\(A\): Productivity of technology. Default value is 2.5.
\(\mu\), \(\sigma\): Mean and standard deviation of the log of the shock. Default values are -0.025 and 0.4, respectively.
\(\beta\): time preference discount factor. Default value is .96.
nb_points_integ: number of points used for integration through Gauss-Hermite quadrature: default value is 10
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
from numba import njit, prange
from quantecon.optimize import root_finding
#=========== Class: BCG for complete markets ===========#
class BCG_complete_markets:
# init method or constructor
def __init__(self,
𝜒1 = 0,
𝜒2 = 0.9,
w10 = 1,
w20 = 1,
𝜃10 = 0.5,
𝜃20 = 0.5,
𝜓 = 3,
𝛼 = 0.6,
A = 2.5,
𝜇 = -0.025,
𝜎 = 0.4,
𝛽 = 0.96,
nb_points_integ = 10):
#=========== Setup ===========#
# Risk parameters
self.𝜒1 = 𝜒1
self.𝜒2 = 𝜒2
# Other parameters
self.𝜓 = 𝜓
self.𝛼 = 𝛼
self.A = A
self.𝜇 = 𝜇
self.𝜎 = 𝜎
self.𝛽 = 𝛽
# Utility
self.u = lambda c: (c**(1-𝜓)) / (1-𝜓)
# Production
self.f = njit(lambda k: A * (k ** 𝛼))
self.Y = lambda 𝜖, k: np.exp(𝜖) * self.f(k)
# Initial endowments
self.w10 = w10
self.w20 = w20
self.w0 = w10 + w20
# Initial holdings
self.𝜃10 = 𝜃10
self.𝜃20 = 𝜃20
# Endowments at t=1
w11 = njit(lambda 𝜖: np.exp(-𝜒1*𝜇 - 0.5*(𝜒1**2)*(𝜎**2) + 𝜒1*𝜖))
w21 = njit(lambda 𝜖: np.exp(-𝜒2*𝜇 - 0.5*(𝜒2**2)*(𝜎**2) + 𝜒2*𝜖))
self.w11 = w11
self.w21 = w21
self.w1 = njit(lambda 𝜖: w11(𝜖) + w21(𝜖))
# Normal PDF
self.g = lambda x: norm.pdf(x, loc=𝜇, scale=𝜎)
# Integration
x, self.weights = np.polynomial.hermite.hermgauss(nb_points_integ)
self.points_integral = np.sqrt(2) * 𝜎 * x + 𝜇
self.k_foc = k_foc_factory(self)
#=========== Optimal k ===========#
# Function: solve for optimal k
def opt_k(self, plot=False):
w0 = self.w0
# Grid for k
kgrid = np.linspace(1e-4, w0-1e-4, 100)
# get FONC values for each k in the grid
kfoc_list = [];
for k in kgrid:
kfoc = self.k_foc(k, self.𝜒1, self.𝜒2)
kfoc_list.append(kfoc)
# Plot FONC for k
if plot:
fig, ax = plt.subplots(figsize=(8,7))
ax.plot(kgrid, kfoc_list, color='blue', label=r'FONC for k')
ax.axhline(0, color='red', linestyle='--')
ax.legend()
ax.set_xlabel(r'k')
plt.show()
# Find k that solves the FONC
kk = root_finding.newton_secant(self.k_foc, 1e-2, args=(self.𝜒1, self.𝜒2)).root
return kk
#=========== Arrow security price ===========#
# Function: Compute Arrow security price
def q(self,𝜖,k):
𝛽 = self.𝛽
𝜓 = self.𝜓
w0 = self.w0
w1 = self.w1
fk = self.f(k)
g = self.g
return 𝛽 * ((w1(𝜖) + np.exp(𝜖)*fk) / (w0 - k))**(-𝜓)
#=========== Firm value V ===========#
# Function: compute firm value V
def V(self, k):
q = self.q
fk = self.f(k)
weights = self.weights
integ = lambda 𝜖: np.exp(𝜖) * fk * q(𝜖, k)
return -k + np.sum(weights * integ(self.points_integral)) / np.sqrt(np.pi)
#=========== Optimal c ===========#
# Function: Compute optimal consumption choices c
def opt_c(self, k=None, plot=False):
w1 = self.w1
w0 = self.w0
w10 = self.w10
w11 = self.w11
𝜃10 = self.𝜃10
Y = self.Y
q = self.q
V = self.V
weights = self.weights
if k is None:
k = self.opt_k()
# Solve for the ratio of consumption 𝜂 from the intertemporal B.C.
fk = self.f(k)
c1 = lambda 𝜖: (w1(𝜖) + np.exp(𝜖)*fk)*q(𝜖,k)
denom = np.sum(weights * c1(self.points_integral)) / np.sqrt(np.pi) + (w0 - k)
w11q = lambda 𝜖: w11(𝜖)*q(𝜖,k)
num = w10 + 𝜃10 * V(k) + np.sum(weights * w11q(self.points_integral)) / np.sqrt(np.pi)
𝜂 = num / denom
# Consumption choices
c10 = 𝜂 * (w0 - k)
c20 = (1-𝜂) * (w0 - k)
c11 = lambda 𝜖: 𝜂 * (w1(𝜖)+Y(𝜖,k))
c21 = lambda 𝜖: (1-𝜂) * (w1(𝜖)+Y(𝜖,k))
return c10, c20, c11, c21
def k_foc_factory(model):
𝜓 = model.𝜓
f = model.f
𝛽 = model.𝛽
𝛼 = model.𝛼
A = model.A
𝜓 = model.𝜓
w0 = model.w0
𝜇 = model.𝜇
𝜎 = model.𝜎
weights = model.weights
points_integral = model.points_integral
w11 = njit(lambda 𝜖, 𝜒1, : np.exp(-𝜒1*𝜇 - 0.5*(𝜒1**2)*(𝜎**2) + 𝜒1*𝜖))
w21 = njit(lambda 𝜖, 𝜒2: np.exp(-𝜒2*𝜇 - 0.5*(𝜒2**2)*(𝜎**2) + 𝜒2*𝜖))
w1 = njit(lambda 𝜖, 𝜒1, 𝜒2: w11(𝜖, 𝜒1) + w21(𝜖, 𝜒2))
@njit
def integrand(𝜖, 𝜒1, 𝜒2, k=1e-4):
fk = f(k)
return (w1(𝜖, 𝜒1, 𝜒2) + np.exp(𝜖) * fk) ** (-𝜓) * np.exp(𝜖)
@njit
def k_foc(k, 𝜒1, 𝜒2):
int_k = np.sum(weights * integrand(points_integral, 𝜒1, 𝜒2, k=k)) / np.sqrt(np.pi)
mul = 𝛽 * 𝛼 * A * k ** (𝛼 - 1) / ((w0 - k) ** (-𝜓))
val = mul * int_k - 1
return val
return k_foc
37.3.1. Examples#
Below we provide some examples of how to use BCG_complete markets.
37.3.1.1. 1st example#
In the first example, we set up instances of BCG complete markets models.
We can use either default parameter values or set parameter values as we want.
The two instances of the BCG complete markets model, mdl1 and
mdl2, represent the model with default parameter settings and with agent 2’s income correlation altered to be \(\chi_2 = -0.9\),
respectively.
# Example: BCG model for complete markets
mdl1 = BCG_complete_markets()
mdl2 = BCG_complete_markets(𝜒2=-0.9)
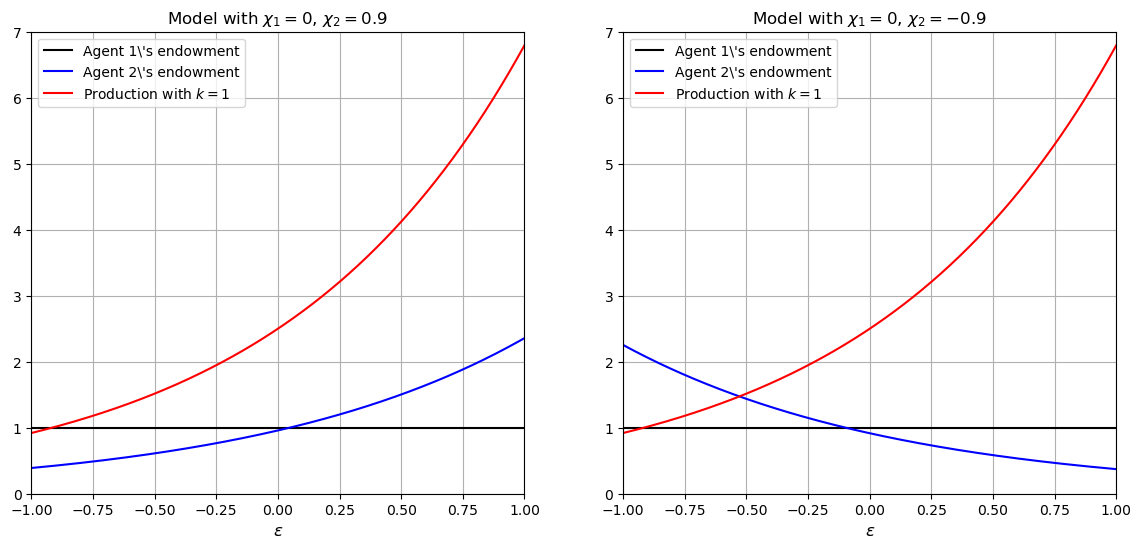
Let’s plot the agents’ time-1 endowments with respect to shocks to see the difference in the two models:
#==== Figure 1: HH endowments and firm productivity ====#
# Realizations of innovation from -3 to 3
epsgrid = np.linspace(-1,1,1000)
fig, ax = plt.subplots(1,2,figsize=(14,6))
ax[0].plot(epsgrid, mdl1.w11(epsgrid), color='black', label='Agent 1\'s endowment')
ax[0].plot(epsgrid, mdl1.w21(epsgrid), color='blue', label='Agent 2\'s endowment')
ax[0].plot(epsgrid, mdl1.Y(epsgrid,1), color='red', label=r'Production with $k=1$')
ax[0].set_xlim([-1,1])
ax[0].set_ylim([0,7])
ax[0].set_xlabel(r'$\epsilon$',fontsize=12)
ax[0].set_title(r'Model with $\chi_1 = 0$, $\chi_2 = 0.9$')
ax[0].legend()
ax[0].grid()
ax[1].plot(epsgrid, mdl2.w11(epsgrid), color='black', label='Agent 1\'s endowment')
ax[1].plot(epsgrid, mdl2.w21(epsgrid), color='blue', label='Agent 2\'s endowment')
ax[1].plot(epsgrid, mdl2.Y(epsgrid,1), color='red', label=r'Production with $k=1$')
ax[1].set_xlim([-1,1])
ax[1].set_ylim([0,7])
ax[1].set_xlabel(r'$\epsilon$',fontsize=12)
ax[1].set_title(r'Model with $\chi_1 = 0$, $\chi_2 = -0.9$')
ax[1].legend()
ax[1].grid()
plt.show()
Let’s also compare the optimal capital stock, \(k\), and optimal time-0 consumption of agent 2, \(c^2_0\), for the two models:
# Print optimal k
kk_1 = mdl1.opt_k()
kk_2 = mdl2.opt_k()
print('The optimal k for model 1: {:.5f}'.format(kk_1))
print('The optimal k for model 2: {:.5f}'.format(kk_2))
# Print optimal time-0 consumption for agent 2
c20_1 = mdl1.opt_c(k=kk_1)[1]
c20_2 = mdl2.opt_c(k=kk_2)[1]
print('The optimal c20 for model 1: {:.5f}'.format(c20_1))
print('The optimal c20 for model 2: {:.5f}'.format(c20_2))
The optimal k for model 1: 0.14235
The optimal k for model 2: 0.13791
The optimal c20 for model 1: 0.90205
The optimal c20 for model 2: 0.92862
37.3.1.2. 2nd example#
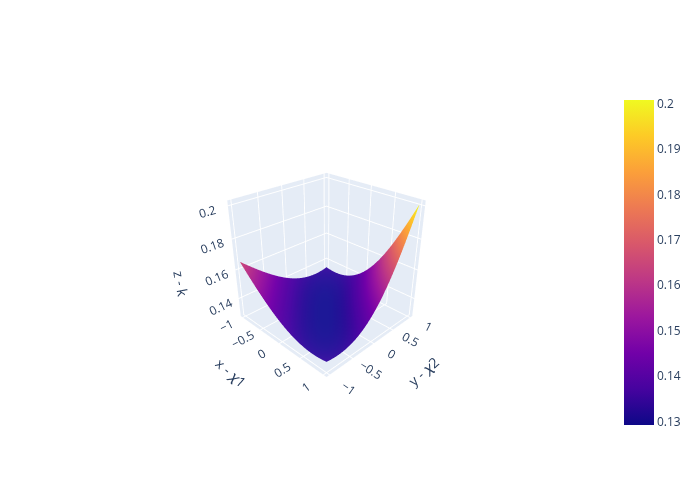
In the second example, we illustrate how the optimal choice of \(k\) is influenced by the correlation parameter \(\chi_i\).
We will need to install the plotly package for 3D illustration. See
https://plotly.com/python/getting-started/ for further instructions.
# Mesh grid of 𝜒
N = 30
𝜒1grid, 𝜒2grid = np.meshgrid(np.linspace(-1,1,N),
np.linspace(-1,1,N))
k_foc = k_foc_factory(mdl1)
# Create grid for k
kgrid = np.zeros_like(𝜒1grid)
w0 = mdl1.w0
@njit(parallel=True)
def fill_k_grid(kgrid):
# Loop: Compute optimal k and
for i in prange(N):
for j in prange(N):
X1 = 𝜒1grid[i, j]
X2 = 𝜒2grid[i, j]
k = root_finding.newton_secant(k_foc, 1e-2, args=(X1, X2)).root
kgrid[i, j] = k
%%time
fill_k_grid(kgrid)
CPU times: user 4.6 s, sys: 112 ms, total: 4.71 s
Wall time: 4.71 s
%%time
# Second-run
fill_k_grid(kgrid)
CPU times: user 8.7 ms, sys: 0 ns, total: 8.7 ms
Wall time: 2.67 ms
#=== Example: Plot optimal k with different correlations ===#
from IPython.display import Image
# Import plotly
import plotly.graph_objs as go
# Plot optimal k
fig = go.Figure(data=[go.Surface(x=𝜒1grid, y=𝜒2grid, z=kgrid)])
fig.update_layout(scene = dict(xaxis_title='x - 𝜒1',
yaxis_title='y - 𝜒2',
zaxis_title='z - k',
aspectratio=dict(x=1,y=1,z=1)))
fig.update_layout(width=500,
height=500,
margin=dict(l=50, r=50, b=65, t=90))
fig.update_layout(scene_camera=dict(eye=dict(x=2, y=-2, z=1.5)))
# Export to PNG file
Image(fig.to_image(format="png"))
# fig.show() will provide interactive plot when running
# notebook locally
