45. Optimal Taxation without State-Contingent Debt#
In addition to what’s in Anaconda, this lecture will need the following libraries:
!pip install --upgrade quantecon
!pip install interpolation
Show code cell output
Requirement already satisfied: quantecon in /home/runner/miniconda3/envs/quantecon/lib/python3.12/site-packages (0.7.2)
Requirement already satisfied: numba>=0.49.0 in /home/runner/miniconda3/envs/quantecon/lib/python3.12/site-packages (from quantecon) (0.60.0)
Requirement already satisfied: numpy>=1.17.0 in /home/runner/miniconda3/envs/quantecon/lib/python3.12/site-packages (from quantecon) (1.26.4)
Requirement already satisfied: requests in /home/runner/miniconda3/envs/quantecon/lib/python3.12/site-packages (from quantecon) (2.32.3)
Requirement already satisfied: scipy>=1.5.0 in /home/runner/miniconda3/envs/quantecon/lib/python3.12/site-packages (from quantecon) (1.13.1)
Requirement already satisfied: sympy in /home/runner/miniconda3/envs/quantecon/lib/python3.12/site-packages (from quantecon) (1.13.2)
Requirement already satisfied: llvmlite<0.44,>=0.43.0dev0 in /home/runner/miniconda3/envs/quantecon/lib/python3.12/site-packages (from numba>=0.49.0->quantecon) (0.43.0)
Requirement already satisfied: charset-normalizer<4,>=2 in /home/runner/miniconda3/envs/quantecon/lib/python3.12/site-packages (from requests->quantecon) (3.3.2)
Requirement already satisfied: idna<4,>=2.5 in /home/runner/miniconda3/envs/quantecon/lib/python3.12/site-packages (from requests->quantecon) (3.7)
Requirement already satisfied: urllib3<3,>=1.21.1 in /home/runner/miniconda3/envs/quantecon/lib/python3.12/site-packages (from requests->quantecon) (2.2.3)
Requirement already satisfied: certifi>=2017.4.17 in /home/runner/miniconda3/envs/quantecon/lib/python3.12/site-packages (from requests->quantecon) (2024.8.30)
Requirement already satisfied: mpmath<1.4,>=1.1.0 in /home/runner/miniconda3/envs/quantecon/lib/python3.12/site-packages (from sympy->quantecon) (1.3.0)
Collecting interpolation
Downloading interpolation-2.2.7-py3-none-any.whl.metadata (913 bytes)
Requirement already satisfied: numba>=0.59.1 in /home/runner/miniconda3/envs/quantecon/lib/python3.12/site-packages (from interpolation) (0.60.0)
Requirement already satisfied: scipy<2.0,>=1.10 in /home/runner/miniconda3/envs/quantecon/lib/python3.12/site-packages (from interpolation) (1.13.1)
Requirement already satisfied: llvmlite<0.44,>=0.43.0dev0 in /home/runner/miniconda3/envs/quantecon/lib/python3.12/site-packages (from numba>=0.59.1->interpolation) (0.43.0)
Requirement already satisfied: numpy<2.1,>=1.22 in /home/runner/miniconda3/envs/quantecon/lib/python3.12/site-packages (from numba>=0.59.1->interpolation) (1.26.4)
Downloading interpolation-2.2.7-py3-none-any.whl (80 kB)
Installing collected packages: interpolation
Successfully installed interpolation-2.2.7
45.1. Overview#
Let’s start with following imports:
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import root
from interpolation.splines import eval_linear, UCGrid, nodes
from quantecon import optimize, MarkovChain
from numba import njit, prange, float64
from numba.experimental import jitclass
In an earlier lecture, we described a model of optimal taxation with state-contingent debt due to Robert E. Lucas, Jr., and Nancy Stokey [Lucas and Stokey, 1983].
Aiyagari, Marcet, Sargent, and Seppälä [Aiyagari et al., 2002] (hereafter, AMSS) studied optimal taxation in a model without state-contingent debt.
In this lecture, we
describe assumptions and equilibrium concepts
solve the model
implement the model numerically
conduct some policy experiments
compare outcomes with those in a corresponding complete-markets model
We begin with an introduction to the model.
45.2. Competitive Equilibrium with Distorting Taxes#
Many but not all features of the economy are identical to those of the Lucas-Stokey economy.
Let’s start with things that are identical.
For \(t \geq 0\), a history of the state is represented by \(s^t = [s_t, s_{t-1}, \ldots, s_0]\).
Government purchases \(g(s)\) are an exact time-invariant function of \(s\).
Let \(c_t(s^t)\), \(\ell_t(s^t)\), and \(n_t(s^t)\) denote consumption, leisure, and labor supply, respectively, at history \(s^t\) at time \(t\).
Each period a representative household is endowed with one unit of time that can be divided between leisure \(\ell_t\) and labor \(n_t\):
Output equals \(n_t(s^t)\) and can be divided between consumption \(c_t(s^t)\) and \(g(s_t)\)
Output is not storable.
The technology pins down a pre-tax wage rate to unity for all \(t, s^t\).
A representative household’s preferences over \(\{c_t(s^t), \ell_t(s^t)\}_{t=0}^\infty\) are ordered by
where
\(\pi_t(s^t)\) is a joint probability distribution over the sequence \(s^t\), and
the utility function \(u\) is increasing, strictly concave, and three times continuously differentiable in both arguments.
The government imposes a flat rate tax \(\tau_t(s^t)\) on labor income at time \(t\), history \(s^t\).
Lucas and Stokey assumed that there are complete markets in one-period Arrow securities; also see smoothing models.
It is at this point that AMSS [Aiyagari et al., 2002] modify the Lucas and Stokey economy.
AMSS allow the government to issue only one-period risk-free debt each period.
Ruling out complete markets in this way is a step in the direction of making total tax collections behave more like that prescribed in Robert Barro (1979) [Barro, 1979] than they do in Lucas and Stokey (1983) [Lucas and Stokey, 1983].
45.2.1. Risk-free One-Period Debt Only#
In period \(t\) and history \(s^t\), let
\(b_{t+1}(s^t)\) be the amount of the time \(t+1\) consumption good that at time \(t\), history \(s^t\) the government promised to pay
\(R_t(s^t)\) be the gross interest rate on risk-free one-period debt between periods \(t\) and \(t+1\)
\(T_t(s^t)\) be a non-negative lump-sum transfer to the representative household 1
That \(b_{t+1}(s^t)\) is the same for all realizations of \(s_{t+1}\) captures its risk-free character.
The market value at time \(t\) of government debt maturing at time \(t+1\) equals \(b_{t+1}(s^t)\) divided by \(R_t(s^t)\).
The government’s budget constraint in period \(t\) at history \(s^t\) is
where \(z_t(s^t)\) is the net-of-interest government surplus.
To rule out Ponzi schemes, we assume that the government is subject to a natural debt limit (to be discussed in a forthcoming lecture).
The consumption Euler equation for a representative household able to trade only one-period risk-free debt with one-period gross interest rate \(R_t(s^t)\) is
Substituting this expression into the government’s budget constraint (45.4) yields:
Components of \(z_t(s^t)\) on the right side depend on \(s^t\), but the left side is required to depend only on \(s^{t-1}\) .
This is what it means for one-period government debt to be risk-free.
Therefore, the right side of equation (45.5) also has to depend only on \(s^{t-1}\).
This requirement will give rise to measurability constraints on the Ramsey allocation to be discussed soon.
If we replace \(b_{t+1}(s^t)\) on the right side of equation (45.5) by the right side of next period’s budget constraint (associated with a particular realization \(s_{t}\)) we get
After making similar repeated substitutions for all future occurrences of government indebtedness, and by invoking a natural debt limit, we arrive at:
Notice how the conditioning sets in equation (45.6) differ: they are \(s^{t-1}\) on the left side and \(s^t\) on the right side.
Now let’s
substitute the resource constraint into the net-of-interest government surplus, and
use the household’s first-order condition \(1-\tau^n_t(s^t)= u_{\ell}(s^t) /u_c(s^t)\) to eliminate the labor tax rate
so that we can express the net-of-interest government surplus \(z_t(s^t)\) as
If we substitute appropriate versions of the right side of (45.7) for \(z_{t+j}(s^{t+j})\) into equation (45.6), we obtain a sequence of implementability constraints on a Ramsey allocation in an AMSS economy.
Expression (45.6) at time \(t=0\) and initial state \(s^0\) was also an implementability constraint on a Ramsey allocation in a Lucas-Stokey economy:
Indeed, it was the only implementability constraint there.
But now we also have a large number of additional implementability constraints
Equation (45.9) must hold for each \(s^t\) for each \(t \geq 1\).
45.2.2. Comparison with Lucas-Stokey Economy#
The expression on the right side of (45.9) in the Lucas-Stokey (1983) economy would equal the present value of a continuation stream of government net-of-interest surpluses evaluated at what would be competitive equilibrium Arrow-Debreu prices at date \(t\).
In the Lucas-Stokey economy, that present value is measurable with respect to \(s^t\).
In the AMSS economy, the restriction that government debt be risk-free imposes that that same present value must be measurable with respect to \(s^{t-1}\).
In a language used in the literature on incomplete markets models, it can be said that the AMSS model requires that at each \((t, s^t)\) what would be the present value of continuation government net-of-interest surpluses in the Lucas-Stokey model must belong to the marketable subspace of the AMSS model.
45.2.3. Ramsey Problem Without State-contingent Debt#
After we have substituted the resource constraint into the utility function, we can express the Ramsey problem as being to choose an allocation that solves
where the maximization is subject to
and
given \(b_0(s^{-1})\).
45.2.3.1. Lagrangian Formulation#
Let \(\gamma_0(s^0)\) be a non-negative Lagrange multiplier on constraint (45.10).
As in the Lucas-Stokey economy, this multiplier is strictly positive when the government must resort to distortionary taxation; otherwise it equals zero.
A consequence of the assumption that there are no markets in state-contingent securities and that a market exists only in a risk-free security is that we have to attach a stochastic process \(\{\gamma_t(s^t)\}_{t=1}^\infty\) of Lagrange multipliers to the implementability constraints (45.11).
Depending on how the constraints bind, these multipliers can be positive or negative:
A negative multiplier \(\gamma_t(s^t)<0\) means that if we could relax constraint (45.11), we would like to increase the beginning-of-period indebtedness for that particular realization of history \(s^t\).
That would let us reduce the beginning-of-period indebtedness for some other history 2.
These features flow from the fact that the government cannot use state-contingent debt and therefore cannot allocate its indebtedness efficiently across future states.
45.2.4. Some Calculations#
It is helpful to apply two transformations to the Lagrangian.
Multiply constraint (45.10) by \(u_c(s^0)\) and the constraints (45.11) by \(\beta^t u_c(s^{t})\).
Then a Lagrangian for the Ramsey problem can be represented as
where
In (45.12), the second equality uses the law of iterated expectations and Abel’s summation formula (also called summation by parts, see this page).
First-order conditions with respect to \(c_t(s^t)\) can be expressed as
and with respect to \(b_t(s^t)\) as
If we substitute \(z_t(s^t)\) from (45.7) and its derivative \(z_c(s^t)\) into the first-order condition (45.14), we find two differences from the corresponding condition for the optimal allocation in a Lucas-Stokey economy with state-contingent government debt.
The term involving \(b_t(s^{t-1})\) in the first-order condition (45.14) does not appear in the corresponding expression for the Lucas-Stokey economy.
This term reflects the constraint that beginning-of-period government indebtedness must be the same across all realizations of next period’s state, a constraint that would not be present if government debt could be state-contingent.
The Lagrange multiplier \(\Psi_t(s^t)\) in the first-order condition (45.14) may change over time in response to realizations of the state, while the multiplier \(\Phi\) in the Lucas-Stokey economy is time-invariant.
We need some code from an earlier lecture on optimal taxation with state-contingent debt sequential allocation implementation:
class SequentialLS:
'''
Class that takes a preference object, state transition matrix,
and state contingent government expenditure plan as inputs, and
solves the sequential allocation problem described above.
It returns optimal allocations about consumption and labor supply,
as well as the multiplier on the implementability constraint Φ.
'''
def __init__(self,
pref,
π=np.full((2, 2), 0.5),
g=np.array([0.1, 0.2])):
# Initialize from pref object attributes
self.β, self.π, self.g = pref.β, π, g
self.mc = MarkovChain(self.π)
self.S = len(π) # Number of states
self.pref = pref
# Find the first best allocation
self.find_first_best()
def FOC_first_best(self, c, g):
'''
First order conditions that characterize
the first best allocation.
'''
pref = self.pref
Uc, Ul = pref.Uc, pref.Ul
n = c + g
l = 1 - n
return Uc(c, l) - Ul(c, l)
def find_first_best(self):
'''
Find the first best allocation
'''
S, g = self.S, self.g
res = root(self.FOC_first_best, np.full(S, 0.5), args=(g,))
if (res.fun > 1e-10).any():
raise Exception('Could not find first best')
self.cFB = res.x
self.nFB = self.cFB + g
def FOC_time1(self, c, Φ, g):
'''
First order conditions that characterize
optimal time 1 allocation problems.
'''
pref = self.pref
Uc, Ucc, Ul, Ull, Ulc = pref.Uc, pref.Ucc, pref.Ul, pref.Ull, pref.Ulc
n = c + g
l = 1 - n
LHS = (1 + Φ) * Uc(c, l) + Φ * (c * Ucc(c, l) - n * Ulc(c, l))
RHS = (1 + Φ) * Ul(c, l) + Φ * (c * Ulc(c, l) - n * Ull(c, l))
diff = LHS - RHS
return diff
def time1_allocation(self, Φ):
'''
Computes optimal allocation for time t >= 1 for a given Φ
'''
pref = self.pref
S, g = self.S, self.g
# use the first best allocation as intial guess
res = root(self.FOC_time1, self.cFB, args=(Φ, g))
if (res.fun > 1e-10).any():
raise Exception('Could not find LS allocation.')
c = res.x
n = c + g
l = 1 - n
# Compute x
I = pref.Uc(c, n) * c - pref.Ul(c, l) * n
x = np.linalg.solve(np.eye(S) - self.β * self.π, I)
return c, n, x
def FOC_time0(self, c0, Φ, g0, b0):
'''
First order conditions that characterize
time 0 allocation problem.
'''
pref = self.pref
Ucc, Ulc = pref.Ucc, pref.Ulc
n0 = c0 + g0
l0 = 1 - n0
diff = self.FOC_time1(c0, Φ, g0)
diff -= Φ * (Ucc(c0, l0) - Ulc(c0, l0)) * b0
return diff
def implementability(self, Φ, b0, s0, cn0_arr):
'''
Compute the differences between the RHS and LHS
of the implementability constraint given Φ,
initial debt, and initial state.
'''
pref, π, g, β = self.pref, self.π, self.g, self.β
Uc, Ul = pref.Uc, pref.Ul
g0 = self.g[s0]
c, n, x = self.time1_allocation(Φ)
res = root(self.FOC_time0, cn0_arr[0], args=(Φ, g0, b0))
c0 = res.x
n0 = c0 + g0
l0 = 1 - n0
cn0_arr[:] = c0.item(), n0.item()
LHS = Uc(c0, l0) * b0
RHS = Uc(c0, l0) * c0 - Ul(c0, l0) * n0 + β * π[s0] @ x
return RHS - LHS
def time0_allocation(self, b0, s0):
'''
Finds the optimal time 0 allocation given
initial government debt b0 and state s0
'''
# use the first best allocation as initial guess
cn0_arr = np.array([self.cFB[s0], self.nFB[s0]])
res = root(self.implementability, 0., args=(b0, s0, cn0_arr))
if (res.fun > 1e-10).any():
raise Exception('Could not find time 0 LS allocation.')
Φ = res.x[0]
c0, n0 = cn0_arr
return Φ, c0, n0
def τ(self, c, n):
'''
Computes τ given c, n
'''
pref = self.pref
Uc, Ul = pref.Uc, pref.Ul
return 1 - Ul(c, 1-n) / Uc(c, 1-n)
def simulate(self, b0, s0, T, sHist=None):
'''
Simulates planners policies for T periods
'''
pref, π, β = self.pref, self.π, self.β
Uc = pref.Uc
if sHist is None:
sHist = self.mc.simulate(T, s0)
cHist, nHist, Bhist, τHist, ΦHist = np.empty((5, T))
RHist = np.empty(T-1)
# Time 0
Φ, cHist[0], nHist[0] = self.time0_allocation(b0, s0)
τHist[0] = self.τ(cHist[0], nHist[0])
Bhist[0] = b0
ΦHist[0] = Φ
# Time 1 onward
for t in range(1, T):
c, n, x = self.time1_allocation(Φ)
τ = self.τ(c, n)
u_c = Uc(c, 1-n)
s = sHist[t]
Eu_c = π[sHist[t-1]] @ u_c
cHist[t], nHist[t], Bhist[t], τHist[t] = c[s], n[s], x[s] / u_c[s], τ[s]
RHist[t-1] = Uc(cHist[t-1], 1-nHist[t-1]) / (β * Eu_c)
ΦHist[t] = Φ
gHist = self.g[sHist]
yHist = nHist
return [cHist, nHist, Bhist, τHist, gHist, yHist, sHist, ΦHist, RHist]
To analyze the AMSS model, we find it useful to adopt a recursive formulation using techniques like those in our lectures on dynamic Stackelberg models and optimal taxation with state-contingent debt.
45.3. Recursive Version of AMSS Model#
We now describe a recursive formulation of the AMSS economy.
We have noted that from the point of view of the Ramsey planner, the restriction to one-period risk-free securities
leaves intact the single implementability constraint on allocations (45.8) from the Lucas-Stokey economy, but
adds measurability constraints (45.6) on functions of tails of allocations at each time and history
We now explore how these constraints alter Bellman equations for a time \(0\) Ramsey planner and for time \(t \geq 1\), history \(s^t\) continuation Ramsey planners.
45.3.1. Recasting State Variables#
In the AMSS setting, the government faces a sequence of budget constraints
where \(R_t(s^t)\) is the gross risk-free rate of interest between \(t\) and \(t+1\) at history \(s^t\) and \(T_t(s^t)\) are non-negative transfers.
Throughout this lecture, we shall set transfers to zero (for some issues about the limiting behavior of debt, this is possibly an important difference from AMSS [Aiyagari et al., 2002], who restricted transfers to be non-negative).
In this case, the household faces a sequence of budget constraints
The household’s first-order conditions are \(u_{c,t} = \beta R_t \mathbb E_t u_{c,t+1}\) and \((1-\tau_t) u_{c,t} = u_{l,t}\).
Using these to eliminate \(R_t\) and \(\tau_t\) from budget constraint (45.16) gives
or
Now define
and represent the household’s budget constraint at time \(t\), history \(s^t\) as
for \(t \geq 1\).
45.3.2. Measurability Constraints#
Write equation (45.18) as
The right side of equation (45.21) expresses the time \(t\) value of government debt in terms of a linear combination of terms whose individual components are measurable with respect to \(s^t\).
The sum of terms on the right side of equation (45.21) must equal \(b_t(s^{t-1})\).
That implies that it has to be measurable with respect to \(s^{t-1}\).
Equations (45.21) are the measurability constraints that the AMSS model adds to the single time \(0\) implementation constraint imposed in the Lucas and Stokey model.
45.3.3. Two Bellman Equations#
Let \(\Pi(s|s_-)\) be a Markov transition matrix whose entries tell probabilities of moving from state \(s_-\) to state \(s\) in one period.
Let
\(V(x_-, s_-)\) be the continuation value of a continuation Ramsey plan at \(x_{t-1} = x_-, s_{t-1} =s_-\) for \(t \geq 1\)
\(W(b, s)\) be the value of the Ramsey plan at time \(0\) at \(b_0=b\) and \(s_0 = s\)
We distinguish between two types of planners:
For \(t \geq 1\), the value function for a continuation Ramsey planner satisfies the Bellman equation
subject to the following collection of implementability constraints, one for each \(s \in {\cal S}\):
A continuation Ramsey planner at \(t \geq 1\) takes \((x_{t-1}, s_{t-1}) = (x_-, s_-)\) as given and before \(s\) is realized chooses \((n_t(s_t), x_t(s_t)) = (n(s), x(s))\) for \(s \in {\cal S}\).
The Ramsey planner takes \((b_0, s_0)\) as given and chooses \((n_0, x_0)\).
The value function \(W(b_0, s_0)\) for the time \(t=0\) Ramsey planner satisfies the Bellman equation
where maximization is subject to
45.3.4. Martingale Supercedes State-Variable Degeneracy#
Let \(\mu(s|s_-) \Pi(s|s_-)\) be a Lagrange multiplier on the constraint (45.23) for state \(s\).
After forming an appropriate Lagrangian, we find that the continuation Ramsey planner’s first-order condition with respect to \(x(s)\) is
Applying an envelope theorem to Bellman equation (45.22) gives
Equations (45.26) and (45.27) imply that
Equation (45.28) states that \(V_x(x, s)\) is a risk-adjusted martingale.
Saying that \(V_x(x, s)\) is a risk-adjusted martingale means that \(V_x(x, s)\) is a martingale with respect to the probability distribution over \(s^t\) sequences that are generated by the twisted transition probability matrix:
Exercise 45.1
Please verify that \(\check \Pi(s|s_-)\) is a valid Markov transition density, i.e., that its elements are all non-negative and that for each \(s_-\), the sum over \(s\) equals unity.
45.3.5. Absence of State Variable Degeneracy#
Along a Ramsey plan, the state variable \(x_t = x_t(s^t, b_0)\) becomes a function of the history \(s^t\) and initial government debt \(b_0\).
In Lucas-Stokey model, we found that
a counterpart to \(V_x(x,s)\) is time-invariant and equal to the Lagrange multiplier on the Lucas-Stokey implementability constraint
time invariance of \(V_x(x,s)\) is the source of a key feature of the Lucas-Stokey model, namely, state variable degeneracy in which \(x_t\) is an exact time-invariant function of \(s_t\).
That \(V_x(x,s)\) varies over time according to a twisted martingale means that there is no state-variable degeneracy in the AMSS model.
In the AMSS model, both \(x\) and \(s\) are needed to describe the state.
This property of the AMSS model transmits a twisted martingale component to consumption, employment, and the tax rate.
45.3.6. Digression on Non-negative Transfers#
Throughout this lecture, we have imposed that transfers \(T_t = 0\).
AMSS [Aiyagari et al., 2002] instead imposed a nonnegativity constraint \(T_t\geq 0\) on transfers.
They also considered a special case of quasi-linear preferences, \(u(c,l)= c + H(l)\).
In this case, \(V_x(x,s)\leq 0\) is a non-positive martingale.
By the martingale convergence theorem \(V_x(x,s)\) converges almost surely.
Furthermore, when the Markov chain \(\Pi(s| s_-)\) and the government expenditure function \(g(s)\) are such that \(g_t\) is perpetually random, \(V_x(x, s)\) almost surely converges to zero.
For quasi-linear preferences, the first-order condition for maximizing (45.22) subject to (45.23) with respect to \(n(s)\) becomes
When \(\mu(s|s_-) = \beta V_x(x(s),x)\) converges to zero, in the limit \(u_l(s)= 1 =u_c(s)\), so that \(\tau(x(s),s) =0\).
Thus, in the limit, if \(g_t\) is perpetually random, the government accumulates sufficient assets to finance all expenditures from earnings on those assets, returning any excess revenues to the household as non-negative lump-sum transfers.
45.3.7. Code#
The recursive formulation is implemented as follows
class AMSS:
# WARNING: THE CODE IS EXTREMELY SENSITIVE TO CHOCIES OF PARAMETERS.
# DO NOT CHANGE THE PARAMETERS AND EXPECT IT TO WORK
def __init__(self, pref, β, Π, g, x_grid, bounds_v):
self.β, self.Π, self.g = β, Π, g
self.x_grid = x_grid
self.n = x_grid[0][2]
self.S = len(Π)
self.bounds = bounds_v
self.pref = pref
self.T_v, self.T_w = bellman_operator_factory(Π, β, x_grid, g,
bounds_v)
self.V_solved = False
self.W_solved = False
def compute_V(self, V, σ_v_star, tol_vfi, maxitr, print_itr):
T_v = self.T_v
self.success = False
V_new = np.zeros_like(V)
Δ = 1.0
for itr in range(maxitr):
T_v(V, V_new, σ_v_star, self.pref)
Δ = np.max(np.abs(V_new - V))
if Δ < tol_vfi:
self.V_solved = True
print('Successfully completed VFI after %i iterations'
% (itr+1))
break
if (itr + 1) % print_itr == 0:
print('Error at iteration %i : ' % (itr + 1), Δ)
V[:] = V_new[:]
self.V = V
self.σ_v_star = σ_v_star
return V, σ_v_star
def compute_W(self, b_0, W, σ_w_star):
T_w = self.T_w
V = self.V
T_w(W, σ_w_star, V, b_0, self.pref)
self.W = W
self.σ_w_star = σ_w_star
self.W_solved = True
print('Succesfully solved the time 0 problem.')
return W, σ_w_star
def solve(self, V, σ_v_star, b_0, W, σ_w_star, tol_vfi=1e-7,
maxitr=1000, print_itr=10):
print("===============")
print("Solve time 1 problem")
print("===============")
self.compute_V(V, σ_v_star, tol_vfi, maxitr, print_itr)
print("===============")
print("Solve time 0 problem")
print("===============")
self.compute_W(b_0, W, σ_w_star)
def simulate(self, s_hist, b_0):
if not (self.V_solved and self.W_solved):
msg = "V and W need to be successfully computed before simulation."
raise ValueError(msg)
pref = self.pref
x_grid, g, β, S = self.x_grid, self.g, self.β, self.S
σ_v_star, σ_w_star = self.σ_v_star, self.σ_w_star
T = len(s_hist)
s_0 = s_hist[0]
# Pre-allocate
n_hist = np.zeros(T)
x_hist = np.zeros(T)
c_hist = np.zeros(T)
τ_hist = np.zeros(T)
b_hist = np.zeros(T)
g_hist = np.zeros(T)
# Compute t = 0
l_0, T_0 = σ_w_star[s_0]
c_0 = (1 - l_0) - g[s_0]
x_0 = (-pref.Uc(c_0, l_0) * (c_0 - T_0 - b_0) +
pref.Ul(c_0, l_0) * (1 - l_0))
n_hist[0] = (1 - l_0)
x_hist[0] = x_0
c_hist[0] = c_0
τ_hist[0] = 1 - pref.Ul(c_0, l_0) / pref.Uc(c_0, l_0)
b_hist[0] = b_0
g_hist[0] = g[s_0]
# Compute t > 0
for t in range(T - 1):
x_ = x_hist[t]
s_ = s_hist[t]
l = np.zeros(S)
T = np.zeros(S)
for s in range(S):
x_arr = np.array([x_])
l[s] = eval_linear(x_grid, σ_v_star[s_, :, s], x_arr)
T[s] = eval_linear(x_grid, σ_v_star[s_, :, S+s], x_arr)
c = (1 - l) - g
u_c = pref.Uc(c, l)
Eu_c = Π[s_] @ u_c
x = u_c * x_ / (β * Eu_c) - u_c * (c - T) + pref.Ul(c, l) * (1 - l)
c_next = c[s_hist[t+1]]
l_next = l[s_hist[t+1]]
x_hist[t+1] = x[s_hist[t+1]]
n_hist[t+1] = 1 - l_next
c_hist[t+1] = c_next
τ_hist[t+1] = 1 - pref.Ul(c_next, l_next) / pref.Uc(c_next, l_next)
b_hist[t+1] = x_ / (β * Eu_c)
g_hist[t+1] = g[s_hist[t+1]]
return c_hist, n_hist, b_hist, τ_hist, g_hist, n_hist
def obj_factory(Π, β, x_grid, g):
S = len(Π)
@njit
def obj_V(σ, state, V, pref):
# Unpack state
s_, x_ = state
l = σ[:S]
T = σ[S:]
c = (1 - l) - g
u_c = pref.Uc(c, l)
Eu_c = Π[s_] @ u_c
x = u_c * x_ / (β * Eu_c) - u_c * (c - T) + pref.Ul(c, l) * (1 - l)
V_next = np.zeros(S)
for s in range(S):
V_next[s] = eval_linear(x_grid, V[s], np.array([x[s]]))
out = Π[s_] @ (pref.U(c, l) + β * V_next)
return out
@njit
def obj_W(σ, state, V, pref):
# Unpack state
s_, b_0 = state
l, T = σ
c = (1 - l) - g[s_]
x = -pref.Uc(c, l) * (c - T - b_0) + pref.Ul(c, l) * (1 - l)
V_next = eval_linear(x_grid, V[s_], np.array([x]))
out = pref.U(c, l) + β * V_next
return out
return obj_V, obj_W
def bellman_operator_factory(Π, β, x_grid, g, bounds_v):
obj_V, obj_W = obj_factory(Π, β, x_grid, g)
n = x_grid[0][2]
S = len(Π)
x_nodes = nodes(x_grid)
@njit(parallel=True)
def T_v(V, V_new, σ_star, pref):
for s_ in prange(S):
for x_i in prange(n):
state = (s_, x_nodes[x_i])
x0 = σ_star[s_, x_i]
res = optimize.nelder_mead(obj_V, x0, bounds=bounds_v,
args=(state, V, pref))
if res.success:
V_new[s_, x_i] = res.fun
σ_star[s_, x_i] = res.x
else:
print("Optimization routine failed.")
bounds_w = np.array([[-9.0, 1.0], [0., 10.]])
def T_w(W, σ_star, V, b_0, pref):
for s_ in prange(S):
state = (s_, b_0)
x0 = σ_star[s_]
res = optimize.nelder_mead(obj_W, x0, bounds=bounds_w,
args=(state, V, pref))
W[s_] = res.fun
σ_star[s_] = res.x
return T_v, T_w
45.4. Examples#
We now turn to some examples.
45.4.1. Anticipated One-Period War#
In our lecture on optimal taxation with state-contingent debt we studied how the government manages uncertainty in a simple setting.
As in that lecture, we assume the one-period utility function
Note
For convenience in matching our computer code, we have expressed utility as a function of \(n\) rather than leisure \(l\).
We first consider a government expenditure process that we studied earlier in a lecture on optimal taxation with state-contingent debt.
Government expenditures are known for sure in all periods except one.
For \(t<3\) or \(t > 3\) we assume that \(g_t = g_l = 0.1\).
At \(t = 3\) a war occurs with probability 0.5.
If there is war, \(g_3 = g_h = 0.2\).
If there is no war \(g_3 = g_l = 0.1\).
A useful trick is to define components of the state vector as the following six \((t,g)\) pairs:
We think of these 6 states as corresponding to \(s=1,2,3,4,5,6\).
The transition matrix is
The government expenditure at each state is
We assume the same utility parameters as in the Lucas-Stokey economy.
This utility function is implemented in the following class.
crra_util_data = [
('β', float64),
('σ', float64),
('γ', float64)
]
@jitclass(crra_util_data)
class CRRAutility:
def __init__(self,
β=0.9,
σ=2,
γ=2):
self.β, self.σ, self.γ = β, σ, γ
# Utility function
def U(self, c, l):
# Note: `l` should not be interpreted as labor, it is an auxiliary
# variable used to conveniently match the code and the equations
# in the lecture
σ = self.σ
if σ == 1.:
U = np.log(c)
else:
U = (c**(1 - σ) - 1) / (1 - σ)
return U - (1-l) ** (1 + self.γ) / (1 + self.γ)
# Derivatives of utility function
def Uc(self, c, l):
return c ** (-self.σ)
def Ucc(self, c, l):
return -self.σ * c ** (-self.σ - 1)
def Ul(self, c, l):
return (1-l) ** self.γ
def Ull(self, c, l):
return -self.γ * (1-l) ** (self.γ - 1)
def Ucl(self, c, l):
return 0
def Ulc(self, c, l):
return 0
The following figure plots Ramsey plans under complete and incomplete markets for both possible realizations of the state at time \(t=3\).
Ramsey outcomes and policies when the government has access to state-contingent debt are represented by black lines and by red lines when there is only a risk-free bond.
Paths with circles are histories in which there is peace, while those with triangle denote war.
# WARNING: DO NOT EXPECT THE CODE TO WORK IF YOU CHANGE PARAMETERS
σ = 2
γ = 2
β = 0.9
Π = np.array([[0, 1, 0, 0, 0, 0],
[0, 0, 1, 0, 0, 0],
[0, 0, 0, 0.5, 0.5, 0],
[0, 0, 0, 0, 0, 1],
[0, 0, 0, 0, 0, 1],
[0, 0, 0, 0, 0, 1]])
g = np.array([0.1, 0.1, 0.1, 0.2, 0.1, 0.1])
x_min = -1.5555
x_max = 17.339
x_num = 300
x_grid = UCGrid((x_min, x_max, x_num))
crra_pref = CRRAutility(β=β, σ=σ, γ=γ)
S = len(Π)
bounds_v = np.vstack([np.hstack([np.full(S, -10.), np.zeros(S)]),
np.hstack([np.ones(S) - g, np.full(S, 10.)])]).T
amss_model = AMSS(crra_pref, β, Π, g, x_grid, bounds_v)
# WARNING: DO NOT EXPECT THE CODE TO WORK IF YOU CHANGE PARAMETERS
V = np.zeros((len(Π), x_num))
V[:] = -nodes(x_grid).T ** 2
σ_v_star = np.ones((S, x_num, S * 2))
σ_v_star[:, :, :S] = 0.0
W = np.empty(len(Π))
b_0 = 1.0
σ_w_star = np.ones((S, 2))
σ_w_star[:, 0] = -0.05
%%time
amss_model.solve(V, σ_v_star, b_0, W, σ_w_star)
===============
Solve time 1 problem
===============
Error at iteration 10 : 1.110064840137854
Error at iteration 20 : 0.30784885876438395
Error at iteration 30 : 0.03221851531398379
Error at iteration 40 : 0.014347598008733087
Error at iteration 50 : 0.0031219444631354065
Error at iteration 60 : 0.0010783647355108172
Error at iteration 70 : 0.0003761255356202753
Error at iteration 80 : 0.0001318127597098595
Error at iteration 90 : 4.650031579878089e-05
Error at iteration 100 : 1.801377708510188e-05
Error at iteration 110 : 6.175872600877597e-06
Error at iteration 120 : 2.4450291853383987e-06
Error at iteration 130 : 1.0836745989450947e-06
Error at iteration 140 : 5.682877084467464e-07
Error at iteration 150 : 3.567560966644123e-07
Error at iteration 160 : 2.5837734796141376e-07
Error at iteration 170 : 2.047536575844333e-07
Error at iteration 180 : 1.7066849622437985e-07
Error at iteration 190 : 1.4622035848788073e-07
Error at iteration 200 : 1.27387780324284e-07
Error at iteration 210 : 1.1226231499961159e-07
Successfully completed VFI after 220 iterations
===============
Solve time 0 problem
===============
Succesfully solved the time 0 problem.
CPU times: user 2min 7s, sys: 1.68 s, total: 2min 9s
Wall time: 1min 27s
# Solve the LS model
ls_model = SequentialLS(crra_pref, g=g, π=Π)
# WARNING: DO NOT EXPECT THE CODE TO WORK IF YOU CHANGE PARAMETERS
s_hist_h = np.array([0, 1, 2, 3, 5, 5, 5])
s_hist_l = np.array([0, 1, 2, 4, 5, 5, 5])
sim_h_amss = amss_model.simulate(s_hist_h, b_0)
sim_l_amss = amss_model.simulate(s_hist_l, b_0)
sim_h_ls = ls_model.simulate(b_0, 0, 7, s_hist_h)
sim_l_ls = ls_model.simulate(b_0, 0, 7, s_hist_l)
fig, axes = plt.subplots(3, 2, figsize=(14, 10))
titles = ['Consumption', 'Labor Supply', 'Government Debt',
'Tax Rate', 'Government Spending', 'Output']
for ax, title, ls_l, ls_h, amss_l, amss_h in zip(axes.flatten(), titles,
sim_l_ls, sim_h_ls,
sim_l_amss, sim_h_amss):
ax.plot(ls_l, '-ok', ls_h, '-^k', amss_l, '-or', amss_h, '-^r',
alpha=0.7)
ax.set(title=title)
ax.grid()
plt.tight_layout()
plt.show()
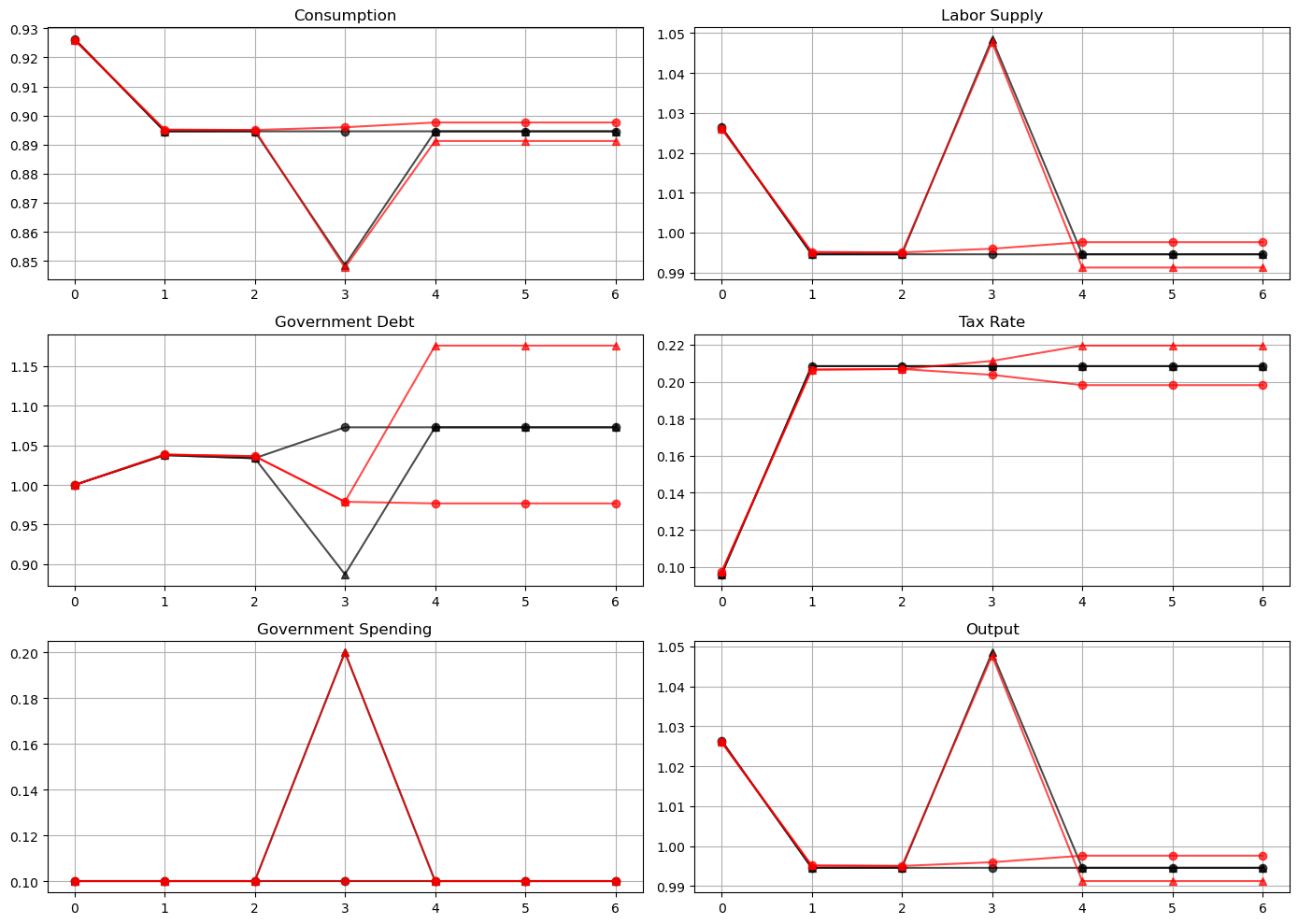
How a Ramsey planner responds to war depends on the structure of the asset market.
If it is able to trade state-contingent debt, then at time \(t=2\)
the government purchases an Arrow security that pays off when \(g_3 = g_h\)
the government sells an Arrow security that pays off when \(g_3 = g_l\)
the Ramsey planner designs these purchases and sales designed so that, regardless of whether or not there is a war at \(t=3\), the government begins period \(t=4\) with the same government debt
This pattern facilities smoothing tax rates across states.
The government without state-contingent debt cannot do this.
Instead, it must enter time \(t=3\) with the same level of debt falling due whether there is peace or war at \(t=3\).
The risk-free rate between time \(2\) and time \(3\) is unusually low because at time \(2\) consumption at time \(3\) is expected to be unusually low.
A low risk-free rate of return on government debt between time \(2\) and time \(3\) allows the government to enter period \(3\) with lower government debt than it entered period \(2\).
To finance a war at time \(3\) it raises taxes and issues more debt to carry into perpetual peace that begins in period \(4\).
To service the additional debt burden, it raises taxes in all future periods.
The absence of state-contingent debt leads to an important difference in the optimal tax policy.
When the Ramsey planner has access to state-contingent debt, the optimal tax policy is history independent
the tax rate is a function of the current level of government spending only, given the Lagrange multiplier on the implementability constraint
Without state-contingent debt, the optimal tax rate is history dependent.
A war at time \(t=3\) causes a permanent increase in the tax rate.
Peace at time \(t=3\) causes a permanent reduction in the tax rate.
45.4.1.1. Perpetual War Alert#
History dependence occurs more dramatically in a case in which the government perpetually faces the prospect of war.
This case was studied in the final example of the lecture on optimal taxation with state-contingent debt.
There, each period the government faces a constant probability, \(0.5\), of war.
In addition, this example features the following preferences
In accordance, we will re-define our utility function.
log_util_data = [
('β', float64),
('ψ', float64)
]
@jitclass(log_util_data)
class LogUtility:
def __init__(self,
β=0.9,
ψ=0.69):
self.β, self.ψ = β, ψ
# Utility function
def U(self, c, l):
return np.log(c) + self.ψ * np.log(l)
# Derivatives of utility function
def Uc(self, c, l):
return 1 / c
def Ucc(self, c, l):
return -c**(-2)
def Ul(self, c, l):
return self.ψ / l
def Ull(self, c, l):
return -self.ψ / l**2
def Ucl(self, c, l):
return 0
def Ulc(self, c, l):
return 0
With these preferences, Ramsey tax rates will vary even in the Lucas-Stokey model with state-contingent debt.
The figure below plots optimal tax policies for both the economy with state-contingent debt (circles) and the economy with only a risk-free bond (triangles).
# WARNING: DO NOT EXPECT THE CODE TO WORK IF YOU CHANGE PARAMETERS
ψ = 0.69
Π = np.full((2, 2), 0.5)
β = 0.9
g = np.array([0.1, 0.2])
x_min = -3.4107
x_max = 3.709
x_num = 300
x_grid = UCGrid((x_min, x_max, x_num))
log_pref = LogUtility(β=β, ψ=ψ)
S = len(Π)
bounds_v = np.vstack([np.zeros(2 * S), np.hstack([1 - g, np.ones(S)]) ]).T
V = np.zeros((len(Π), x_num))
V[:] = -(nodes(x_grid).T + x_max) ** 2 / 14
σ_v_star = 1 - np.full((S, x_num, S * 2), 0.55)
W = np.empty(len(Π))
b_0 = 0.5
σ_w_star = 1 - np.full((S, 2), 0.55)
amss_model = AMSS(log_pref, β, Π, g, x_grid, bounds_v)
%%time
amss_model.solve(V, σ_v_star, b_0, W, σ_w_star, tol_vfi=3e-5, maxitr=3000,
print_itr=100)
===============
Solve time 1 problem
===============
Error at iteration 100 : 0.0011569123052908026
Error at iteration 200 : 0.0005024948171925558
Error at iteration 300 : 0.0002995649778405607
Error at iteration 400 : 0.00020753209923363158
Error at iteration 500 : 0.00015556566848218267
Error at iteration 600 : 0.0001228034492957164
Error at iteration 700 : 0.00010068689697462219
Error at iteration 800 : 8.474340939912395e-05
Error at iteration 900 : 7.290920770763876e-05
Error at iteration 1000 : 6.375694017535238e-05
Error at iteration 1100 : 5.642689428775327e-05
Error at iteration 1200 : 5.045426282634935e-05
Error at iteration 1300 : 4.561168914030134e-05
Error at iteration 1400 : 4.150059282892471e-05
Error at iteration 1500 : 3.799110186264443e-05
Error at iteration 1600 : 3.5163266918658564e-05
Error at iteration 1700 : 3.263979350620616e-05
Error at iteration 1800 : 3.0359381506528393e-05
Successfully completed VFI after 1818 iterations
===============
Solve time 0 problem
===============
Succesfully solved the time 0 problem.
CPU times: user 1min 58s, sys: 1.35 s, total: 2min
Wall time: 1min 29s
ls_model = SequentialLS(log_pref, g=g, π=Π) # Solve sequential problem
# WARNING: DO NOT EXPECT THE CODE TO WORK IF YOU CHANGE PARAMETERS
s_hist = np.array([0, 0, 0, 0, 0, 0, 0, 0, 1, 1,
0, 0, 0, 1, 1, 1, 1, 1, 1, 0])
T = len(s_hist)
sim_amss = amss_model.simulate(s_hist, b_0)
sim_ls = ls_model.simulate(0.5, 0, T, s_hist)
titles = ['Consumption', 'Labor Supply', 'Government Debt',
'Tax Rate', 'Government Spending', 'Output']
fig, axes = plt.subplots(3, 2, figsize=(14, 10))
for ax, title, ls, amss in zip(axes.flatten(), titles, sim_ls, sim_amss):
ax.plot(ls, '-ok', amss, '-^b')
ax.set(title=title)
ax.grid()
axes[0, 0].legend(('Complete Markets', 'Incomplete Markets'))
plt.tight_layout()
plt.show()
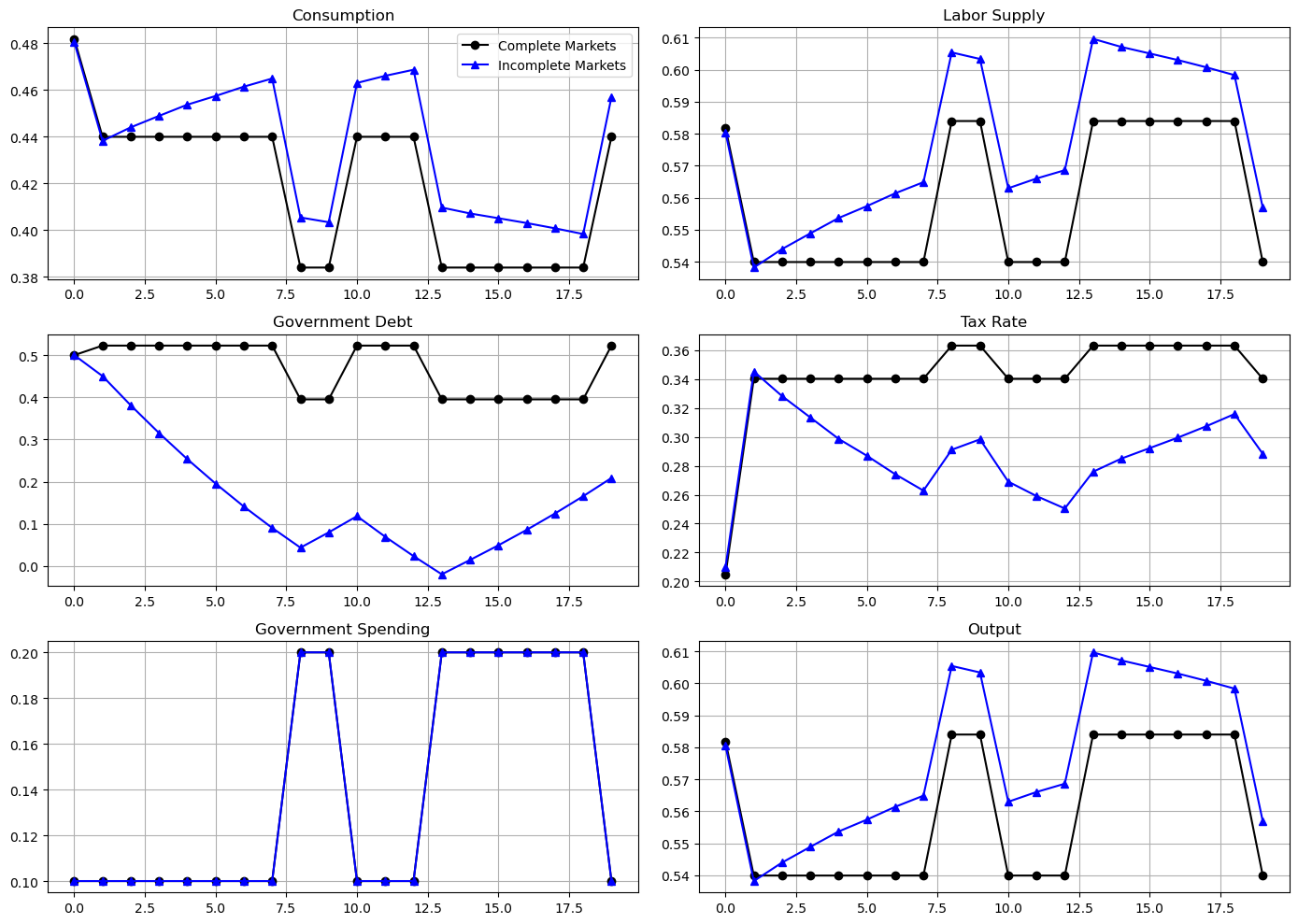
When the government experiences a prolonged period of peace, it is able to reduce government debt and set persistently lower tax rates.
However, the government finances a long war by borrowing and raising taxes.
This results in a drift away from policies with state-contingent debt that depends on the history of shocks.
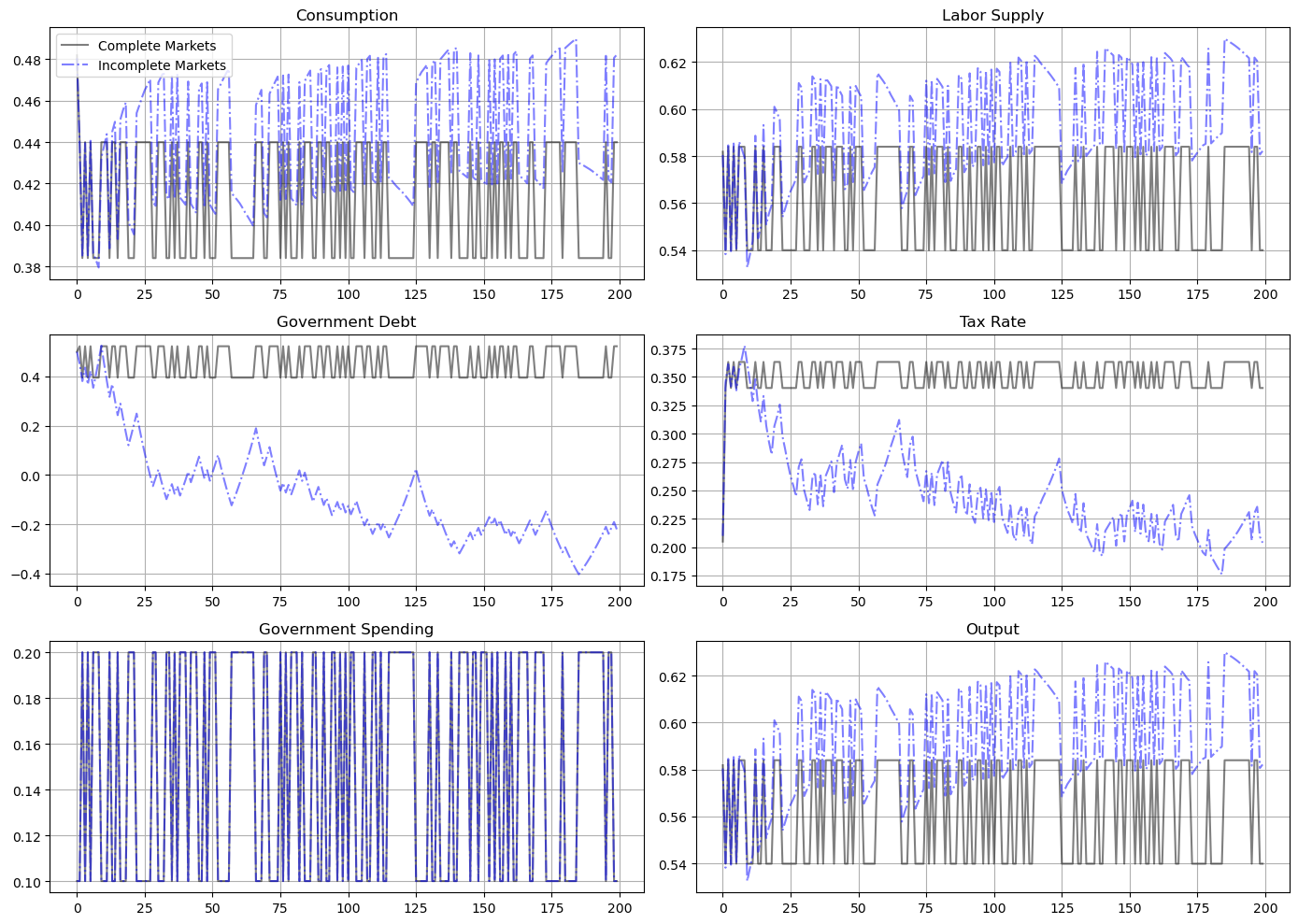
This is even more evident in the following figure that plots the evolution of the two policies over 200 periods.
This outcome reflects the presence of a force for precautionary saving that the incomplete markets structure imparts to the Ramsey plan.
In this subsequent lecture and this subsequent lecture, some ultimate consequences of that force are explored.
T = 200
s_0 = 0
mc = MarkovChain(Π)
s_hist_long = mc.simulate(T, init=s_0, random_state=5)
sim_amss = amss_model.simulate(s_hist_long, b_0)
sim_ls = ls_model.simulate(0.5, 0, T, s_hist_long)
titles = ['Consumption', 'Labor Supply', 'Government Debt',
'Tax Rate', 'Government Spending', 'Output']
fig, axes = plt.subplots(3, 2, figsize=(14, 10))
for ax, title, ls, amss in zip(axes.flatten(), titles, sim_ls, \
sim_amss):
ax.plot(ls, '-k', amss, '-.b', alpha=0.5)
ax.set(title=title)
ax.grid()
axes[0, 0].legend(('Complete Markets','Incomplete Markets'))
plt.tight_layout()
plt.show()
- 1
In an allocation that solves the Ramsey problem and that levies distorting taxes on labor, why would the government ever want to hand revenues back to the private sector? It would not in an economy with state-contingent debt, since any such allocation could be improved by lowering distortionary taxes rather than handing out lump-sum transfers. But, without state-contingent debt there can be circumstances when a government would like to make lump-sum transfers to the private sector.
- 2
From the first-order conditions for the Ramsey problem, there exists another realization \(\tilde s^t\) with the same history up until the previous period, i.e., \(\tilde s^{t-1}= s^{t-1}\), but where the multiplier on constraint (45.11) takes a positive value, so \(\gamma_t(\tilde s^t)>0\).