21. Rosen Schooling Model#

This lecture is yet another part of a suite of lectures that use the quantecon DLE class to instantiate models within the [Hansen and Sargent, 2013] class of models described in detail in Recursive Models of Dynamic Linear Economies.

In addition to what’s included in Anaconda, this lecture uses the quantecon library

!pip install --upgrade quantecon

We’ll also need the following imports:

import numpy as np
import matplotlib.pyplot as plt
from collections import namedtuple
from quantecon import DLE

21.1. A One-Occupation Model#

Ryoo and Rosen’s (2004) [Ryoo and Rosen, 2004] partial equilibrium model determines

a stock of “Engineers” \(N_t\)
a number of new entrants in engineering school, \(n_t\)
the wage rate of engineers, \(w_t\)

It takes k periods of schooling to become an engineer.

The model consists of the following equations:

a demand curve for engineers:

\[ w_t = - \alpha_d N_t + \epsilon_{dt} \]

a time-to-build structure of the education process:

\[ N_{t+k} = \delta_N N_{t+k-1} + n_t \]

a definition of the discounted present value of each new engineering student:

\[ v_t = \beta_k \mathbb{E} \sum_{j=0}^\infty (\beta \delta_N)^j w_{t+k+j} \]

a supply curve of new students driven by present value \(v_t\):

\[ n_t = \alpha_s v_t + \epsilon_{st} \]

21.2. Mapping into HS2013 Framework#

We represent this model in the [Hansen and Sargent, 2013] framework by

sweeping the time-to-build structure and the demand for engineers into the household technology, and
putting the supply of engineers into the technology for producing goods

21.2.1. Preferences#

\[\begin{split} \Pi = 0, \Lambda= \begin{bmatrix} \alpha_d & 0 & \cdots & 0 \end{bmatrix} , \Delta_h = \begin{bmatrix} \delta_N & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots& \cdots & 0 & 1 \\ 0 & 0 & 0 & \cdots & 0 \end{bmatrix} , \Theta_h = \begin{bmatrix} 0 \\ 0 \\ \vdots \\ 0 \\ 1 \end{bmatrix} \end{split}\]

where \(\Lambda\) is a k+1 x 1 matrix, \(\Delta_h\) is a k_1 x k+1 matrix, and \(\Theta_h\) is a k+1 x 1 matrix.

This specification sets \(N_t = h_{1t-1}\), \(n_t = c_t\), \(h_{\tau+1,t-1} = n_{t-(k-\tau)}\) for \(\tau = 1,...,k\).

Below we set things up so that the number of years of education, \(k\), can be varied.

21.2.2. Technology#

To capture Ryoo and Rosen’s [Ryoo and Rosen, 2004] supply curve, we use the physical technology:

\[ c_t = i_t + d_{1t} \]

\[ \psi_1i_t = g_t \]

where \(\psi_1\) is inversely proportional to \(\alpha_s\).

21.2.3. Information#

Because we want \(b_t = \epsilon_{dt}\) and \(d_{1t} =\epsilon_{st}\), we set

\[\begin{split} A_{22}= \begin{bmatrix} 1 & 0 & 0 \\ 0 & \rho_s & 0 \\ 0 & 0 & \rho_d \end{bmatrix} , C_2 = \begin{bmatrix} 0 & 0 \\ 1 & 0 \\ 0 & 1 \end{bmatrix} , U_b = \begin{bmatrix} 30 & 0 & 1 \end{bmatrix} , U_d = \begin{bmatrix} 10 & 1 & 0 \\ 0 & 0 & 0 \end{bmatrix} \end{split}\]

where \(\rho_s\) and \(\rho_d\) describe the persistence of the supply and demand shocks

Information = namedtuple('Information', ['a22', 'c2','ub','ud'])
Technology = namedtuple('Technology', ['ϕ_c', 'ϕ_g', 'ϕ_i', 'γ', 'δ_k', 'θ_k'])
Preferences = namedtuple('Preferences', ['β', 'l_λ', 'π_h', 'δ_h', 'θ_h'])

21.2.4. Effects of Changes in Education Technology and Demand#

We now study how changing

the number of years of education required to become an engineer and
the slope of the demand curve

affects responses to demand shocks.

To begin, we set \(k = 4\) and \(\alpha_d = 0.1\)

k = 4  # Number of periods of schooling required to become an engineer

β = np.array([[1 / 1.05]])
α_d = np.array([[0.1]])
α_s = 1
ε_1 = 1e-7
λ_1 = np.full((1, k), ε_1)
# Use of ε_1 is trick to aquire detectability, see HS2013 p. 228 footnote 4
l_λ = np.hstack((α_d, λ_1))
π_h = np.array([[0]])

δ_n = np.array([[0.95]])
d1 = np.vstack((δ_n, np.zeros((k - 1, 1))))
d2 = np.hstack((d1, np.eye(k)))
δ_h = np.vstack((d2, np.zeros((1, k + 1))))

θ_h = np.vstack((np.zeros((k, 1)),
                 np.ones((1, 1))))

ψ_1 = 1 / α_s

ϕ_c = np.array([[1], [0]])
ϕ_g = np.array([[0], [-1]])
ϕ_i = np.array([[-1], [ψ_1]])
γ = np.array([[0], [0]])

δ_k = np.array([[0]])
θ_k = np.array([[0]])

ρ_s = 0.8
ρ_d = 0.8

a22 = np.array([[1,   0,   0],
                [0, ρ_s,   0],
                [0,   0, ρ_d]])

c2 = np.array([[0, 0], [10, 0], [0, 10]])
ub = np.array([[30, 0, 1]])
ud = np.array([[10, 1, 0], [0, 0, 0]])

info1 = Information(a22, c2, ub, ud)
tech1 = Technology(ϕ_c, ϕ_g, ϕ_i, γ, δ_k, θ_k)
pref1 = Preferences(β, l_λ, π_h, δ_h, θ_h)

econ1 = DLE(info1, tech1, pref1)

We create three other instances by:

Raising \(\alpha_d\) to 2
Raising \(k\) to 7
Raising \(k\) to 10

α_d = np.array([[2]])
l_λ = np.hstack((α_d, λ_1))
pref2 = Preferences(β, l_λ, π_h, δ_h, θ_h)
econ2 = DLE(info1, tech1, pref2)

α_d = np.array([[0.1]])

k = 7
λ_1 = np.full((1, k), ε_1)
l_λ = np.hstack((α_d, λ_1))
d1 = np.vstack((δ_n, np.zeros((k - 1, 1))))
d2 = np.hstack((d1, np.eye(k)))
δ_h = np.vstack((d2, np.zeros((1, k+1))))
θ_h = np.vstack((np.zeros((k, 1)),
                 np.ones((1, 1))))

Pref3 = Preferences(β, l_λ, π_h, δ_h, θ_h)
econ3 = DLE(info1, tech1, Pref3)

k = 10
λ_1 = np.full((1, k), ε_1)
l_λ = np.hstack((α_d, λ_1))
d1 = np.vstack((δ_n, np.zeros((k - 1, 1))))
d2 = np.hstack((d1, np.eye(k)))
δ_h = np.vstack((d2, np.zeros((1, k + 1))))
θ_h = np.vstack((np.zeros((k, 1)),
                 np.ones((1, 1))))

pref4 = Preferences(β, l_λ, π_h, δ_h, θ_h)
econ4 = DLE(info1, tech1, pref4)

shock_demand = np.array([[0], [1]])

econ1.irf(ts_length=25, shock=shock_demand)
econ2.irf(ts_length=25, shock=shock_demand)
econ3.irf(ts_length=25, shock=shock_demand)
econ4.irf(ts_length=25, shock=shock_demand)

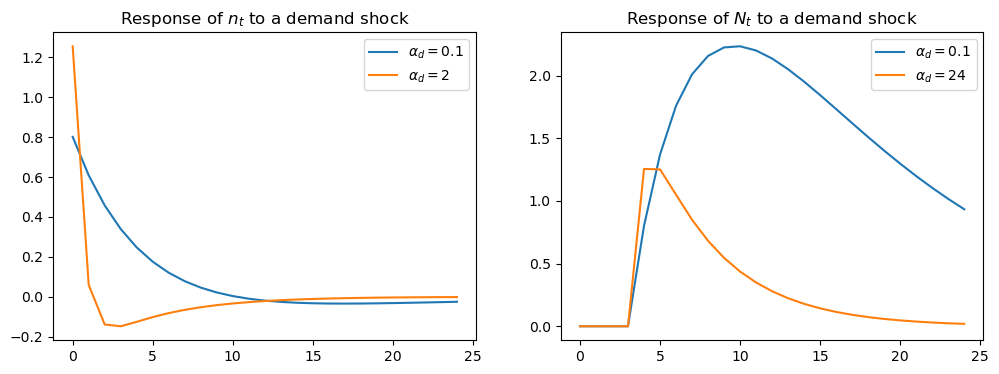
The first figure plots the impulse response of \(n_t\) (on the left) and \(N_t\) (on the right) to a positive demand shock, for \(\alpha_d = 0.1\) and \(\alpha_d = 2\).

When \(\alpha_d = 2\), the number of new students \(n_t\) rises initially, but the response then turns negative.

A positive demand shock raises wages, drawing new students into the profession.

However, these new students raise \(N_t\).

The higher is \(\alpha_d\), the larger the effect of this rise in \(N_t\) on wages.

This counteracts the demand shock’s positive effect on wages, reducing the number of new students in subsequent periods.

Consequently, when \(\alpha_d\) is lower, the effect of a demand shock on \(N_t\) is larger

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
ax1.plot(econ1.c_irf,label='$\\alpha_d = 0.1$')
ax1.plot(econ2.c_irf,label='$\\alpha_d = 2$')
ax1.legend()
ax1.set_title('Response of $n_t$ to a demand shock')

ax2.plot(econ1.h_irf[:, 0], label='$\\alpha_d = 0.1$')
ax2.plot(econ2.h_irf[:, 0], label='$\\alpha_d = 24$')
ax2.legend()
ax2.set_title('Response of $N_t$ to a demand shock')
plt.show()

_images/1e29f287a8e070496a9b4e4c6369018fdd431d65111028d3b265b6b93d518a9a.png

The next figure plots the impulse response of \(n_t\) (on the left) and \(N_t\) (on the right) to a positive demand shock, for \(k=4\), \(k=7\) and \(k=10\) (with \(\alpha_d = 0.1\))

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
ax1.plot(econ1.c_irf, label='$k=4$')
ax1.plot(econ3.c_irf, label='$k=7$')
ax1.plot(econ4.c_irf, label='$k=10$')
ax1.legend()
ax1.set_title('Response of $n_t$ to a demand shock')

ax2.plot(econ1.h_irf[:,0], label='$k=4$')
ax2.plot(econ3.h_irf[:,0], label='$k=7$')
ax2.plot(econ4.h_irf[:,0], label='$k=10$')
ax2.legend()
ax2.set_title('Response of $N_t$ to a demand shock')
plt.show()

_images/31ae6cbc7daf3cb0152ee48e5fcdfb09bd592faf4b70658213d87707511d6b62.png

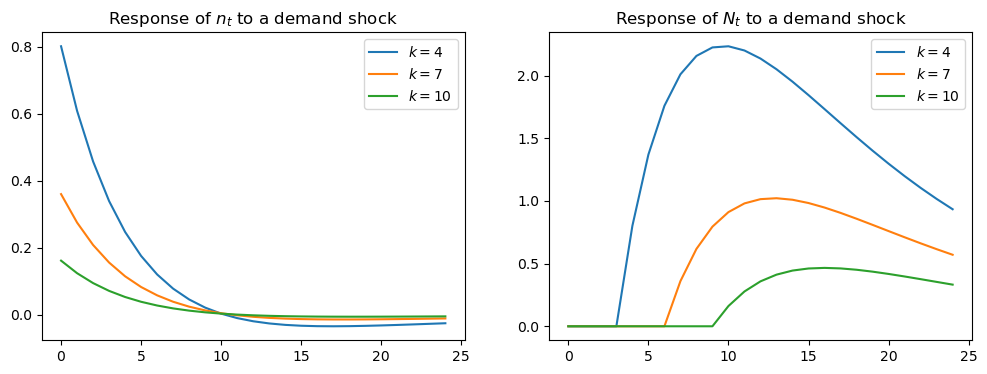
Both panels in the above figure show that raising \(k\) lowers the effect of a positive demand shock on entry into the engineering profession.

Increasing the number of periods of schooling lowers the number of new students in response to a demand shock.

This occurs because with longer required schooling, new students ultimately benefit less from the impact of that shock on wages.